Find the Volume of a Cone

We all like an ice cream cone, the bigger the better!

 

 

To find out how much ice cream we can get into a cone so that it is level with the top, we need to work out the volume.

As ever with shape questions, there is a formula to help us:

 

 

It can be a bother having to learn so many formulas, but let us look at this closely.

 

A cone has a circular shape, so the formula for finding an area of a circle is in it:  π x radius x radius

Now we want to cram as much ice cream into this cone as possible, so we are very interested in its height.

So far we have π x radius² x height. 

This just leaves us with the first part of the formula to learn which is 1/3.

One way to remember this is that there are 3 things to do already, I just have to remember 1 more!

 

When working with the volume of more complex shapes, use the π button on your calculator because it will use π to so many decimal places.  If you use 3.142 or 3.14, answers may differ slightly.

 

Let's get started.

 

 

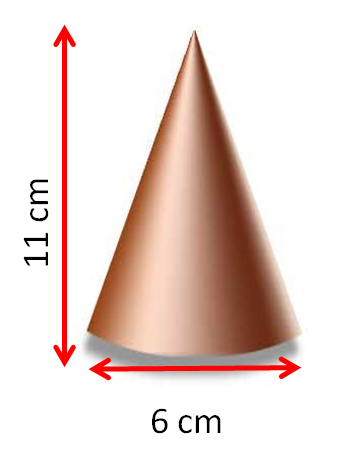
Find the volume of this cone.

 

Just beware of a few things to look out for:

Sometimes you are given the diameter of the cone, remember to halve it to get the radius.

Sometimes you are given two heights, a slanted height and a vertical height. You always work with the vertical height when finding the volume.

Volume is always measured in units³

 

The beauty of this is that you can just put the whole thing into your calculator in one go:

The radius is half of the diameter: 3 cm and the height is 11 cm.

1 ÷ 3 x π x 3²  (or 3 x 3) x 11 = 103.67 cm²   (rounded to 2 decimal places or 2 d.p)

 

Now let's try some questions.