Use Volume Scale Factors to Solve Problems

You should be familiar with the concept of scale factor and calculating lengths of similar shapes.

Here, we will look at questions involving volume scale factor .

 

Example

These two cubes are similar.

 

         

 

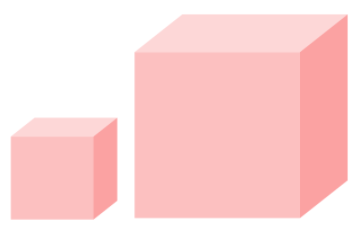
Smaller cube length = 4 cm 

Volume of the smaller cube = 64 cm³ 

 

Larger cube length = 8 cm

                           

What is the volume of the larger cube?

 

Method

1.  Find the scale factor of length by dividing corresponding lengths. 8 ÷ 4  = 2

2.  Cube the scale factor 2 x 2 x 2 = 8

3. Multiply by the volume if you are finding the larger shape, or divide if you want the smaller shape. (In this case, we want the larger shape, so we multiply) 64 x 8  = 512 cm³

 

The step that students tend to forget is Step 2. You must be able to recall that a scale factor of length needs to be cubed in order to make a comparison of two shapes' volumes. 

 

Example 2

 

             

 

Large cuboid length = 18 cm   

Volume of large cuboid = 1620 cm³ 

 

Small cuboid length = 6 cm

What is the volume of the small cuboid?

 

Method

1.  Find the scale factor of length by dividing corresponding lengths. 18 ÷ 6  = 3

2.  Cube the scale factor 3 x 3 x 3 = 27

3. Multiply by the volume if you are finding the larger shape, or divide if you want the smaller shape. (In this case, we want the smaller shape, so we divide) 1620 ÷ 27  = 60 cm³

 

Knowing cube numbers comes in very useful in these types of question. Just remember the steps in the method and you will be able to find unknown volumes of similar shapes.