Find the Surface Area of a Cuboid

 

The best part about a present when you were younger? Yes -  the box. 

All the care taken to wrap up the present when you might as well have just been given an empty box to play with.

The cuboid is a great shape for putting presents in - the shape makes it easier to wrap.

Have you ever wondered how much paper to buy to make sure the whole box is covered?

This is where surface area comes in.

 

The surface area of a shape is just the area of each face added together.

 

 

Cuboids can be found everywhere: house bricks, books, cameras, cookers - they all have to be wrapped to be transported to shops. Can you think of any more?

Retailers have to be able to calculate the surface area so that they can wrap goods before they are shipped off.

 

The surface area of a cuboid  is simply the area of each face added together.

 

Find the surface area of this cuboid:

 

 

 

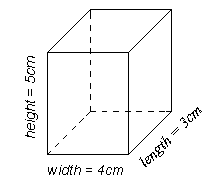
First, find the area of the face we are looking directly at:   5 x 4 = 20 cm²

There is another face exactly the same on the opposite side of the cuboid.  No working out necessary we have already done it.

We now have: face 1 = 20 cm²

                       face 2 = 20 cm²

 

Now let's look at the face on the right-hand side and work out the area: 3 x 5 = 15 cm² 

The opposite face is also the same.

We now have: face 1 = 20 cm²

                      face 2 = 20 cm²

                      face 3 = 15 cm²

                      face 4 = 15 cm²   

 

Now find the remaining two faces in the same way:  4 x 3 = 12 cm²      

We now have: face 1 = 20 cm²

                      face 2 = 20 cm²

                      face 3 = 15 cm²

                      face 4 = 15 cm²  

                     face 5 = 12 cm²

                     face 6 = 12 cm²

Total surface area  = 94 cm²

 

And remember that measurement to do with area is measured in units squared.

 

Happy wrapping.