Find the Surface Area of a Cylinder

Look at this cylinder.

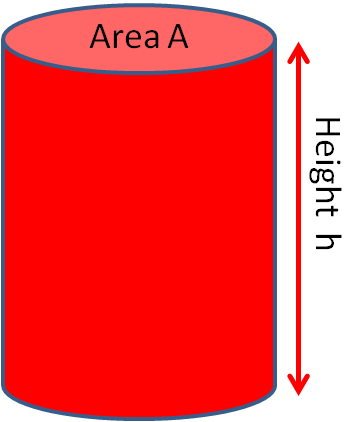
Its net is made up of two circles and a rectangle.

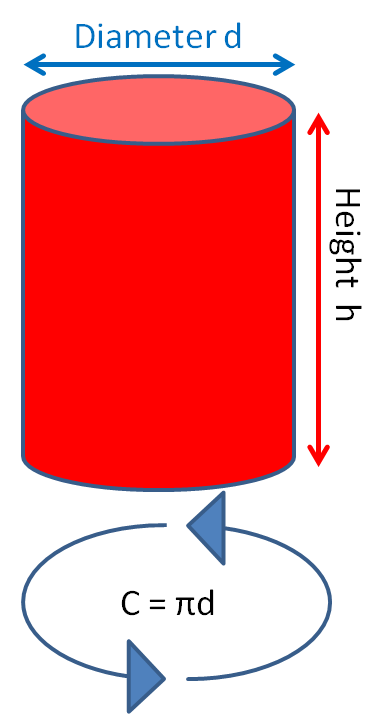
In the two formulae below, r is the radius and d is the diameter.

The area of a circle is πr² 

The circumference of a circle is πd

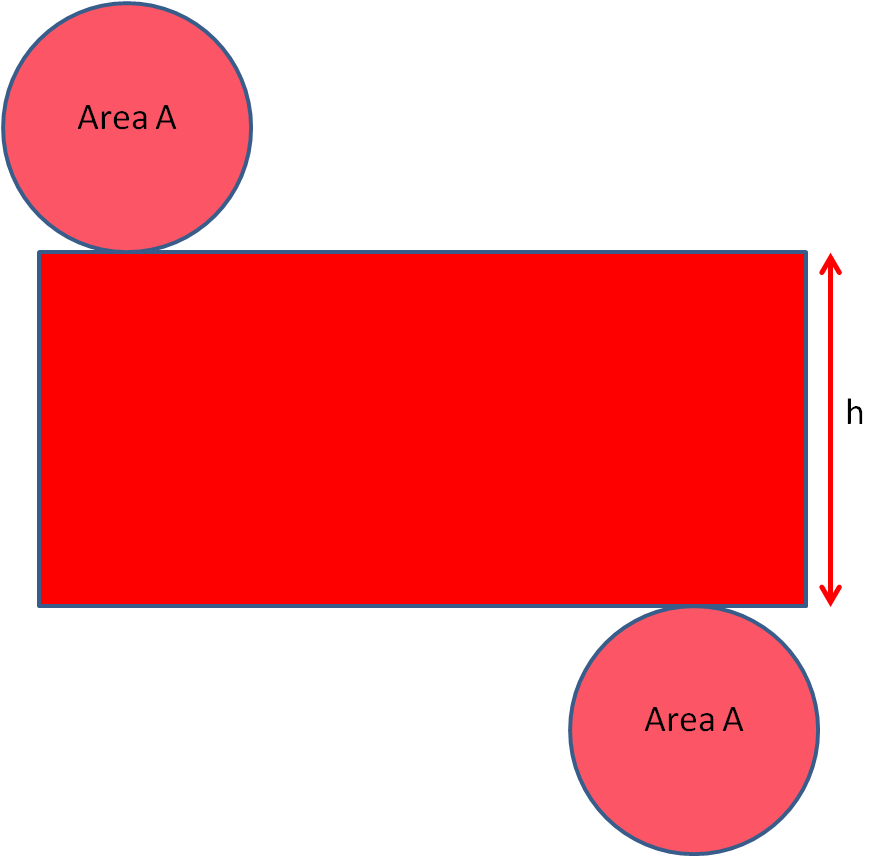
Look at these diagrams to see that the base of the rectangle has the same length as the circumference of the circle. 

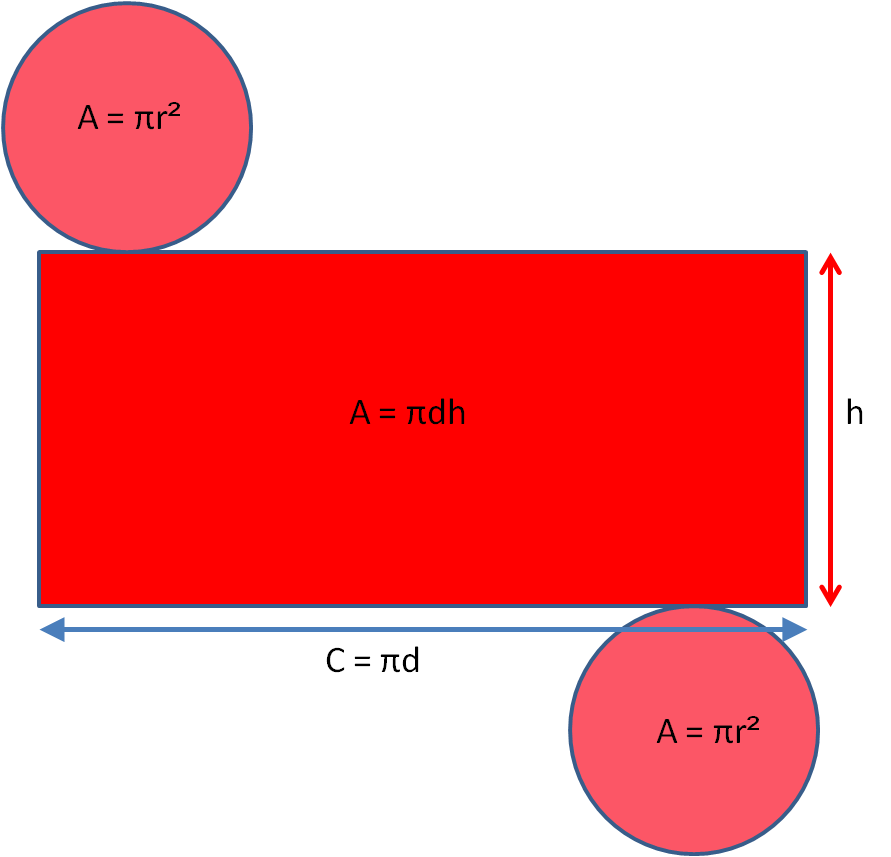
So the surface area is the area of the two circles plus the area of the rectangle.

The area of the two circles = 2πr²

The area of the rectangle =  πdh  or we can write 2πrh (because the diameter is the radius x 2)

 Surface Area = 2πr² + πdh = 2πr² + 2πrh

Example

Find the surface area of this cylinder in cm² to 3 significant figures.

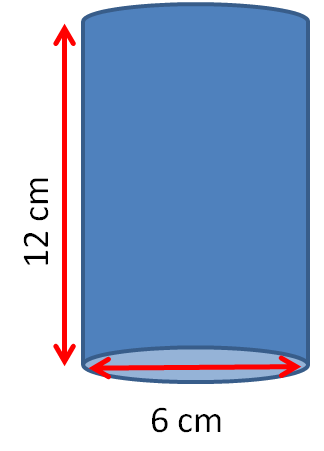
Answer

Diameter = 6 cm

Radius = 6 ÷ 2 = 3 cm

Height = 12 cm

Surface Area = 2πr² + 2πrh  = 2 x π x 3² + 2 x π x 3 x 12 = 282.74 ≈ 283 cm² (3 s.f.)

Let's get started.