Find the LCM and HCF Using the Product of Prime Factors

In this activity, we will be finding the lowest common multiple (LCM) and the highest common factor (HCF) of two numbers using the products of their prime factors.

 

Here's a reminder of how to do this using factor trees.

 

We want to express 36 as the product of prime factors:

 

 

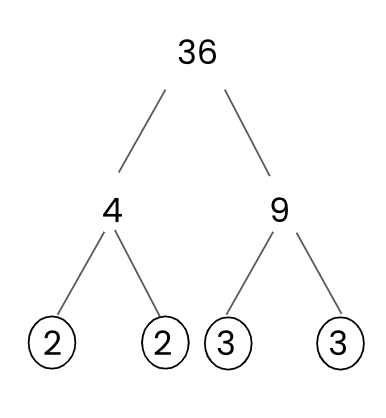
36 has been split into its factor pair of 4 and 9.

4 has been split into its factor pair of 2 and 2. Both are prime numbers, so they have been circled.

9 has been split into its factor pair of 3 and 3. Both are prime numbers, so they have been circled.

So, the prime factors of 36 are 2, 2, 3 and 3.

36 as a product of its prime factors is: 3 x 3 x 2 x 2 or 3² x 2²

 

Once we know the prime factors of two numbers, it is possible to find the LCM and the HCF for them both.

 

Let's say we had to find the LCM and HCF of 36 and 198. We already have 36 as a product of its prime factors, so we would need to do a factor tree for 198 too.

 

Put 198 at the top of the factor tree and work your way down the branches until you have only prime factors.

 

You should end up with 198 = 11 x 3 x 3 x 2 or 11 x 3² x 2

 

Let's write the two numbers above each other, so it is easy to compare factors.

 

36 = 3 x 3 x 2 x 2

198 = 11 x 3 x 3 x 2

 

To find the HCF, we multiply together all the prime factors that appear in both of the lists above.

This is 3 x 3 x 2 = 18

So, the HCF of 36 and 198 is 18.

 

To find the LCM, we multiply together all the prime factors that appear in either list.

This is 11 x 3 x 3 x 2 (from 198) and one more 2 (from 36)

11 x 3 x 3 x 2 x 2 = 396

So, the LCM of 36 and 198 is 396.

 

This is easier than it looks and the best thing to do is to practise some - so, let's get started!

 

You can check back to these instructions at any point by clicking on the red button at the side of the screen.