In this activity, we will write numbers as the products of prime factors.
Method
All whole numbers, other than primes and the number 1, can be written as the product of their prime factors.
We find the prime factors of a number by successively dividing the number by its factor pairs.
Example
Write 1,800 as the product of its prime factors.
The best way to find the prime factors is to divide 1,800 using a factor tree.
Start with 1,800 at the top of the tree and draw two branches coming from the top. This pair of branches will carry a factor pair that multiply together to make 1,800. Let's use 180 x 10
Neither 180 nor 10 are prime numbers, so we draw a pair of branches coming from each of them.
180 could have 18 and 10 as its factor pair.
10 would have 5 and 2 as its factor pair. Both 5 and 2 are prime numbers, so we either circle or underline those two numbers - we can't go any further with those.
Now we go to the other factor pair of 18 and 10. Neither of them are prime numbers, so we need to draw a pair of branches from each of them.
18 could have 9 and 2 as its factor pair.
2 is a prime number, so we underline it.
9 is not a prime number but we'll come back to that in a minute!
10 would have 5 and 2 as its factor pair, as we saw earlier. Both are prime numbers, so we underline both 5 and 2.
Finally, we go back to 9. We draw another pair of branches coming from 9 and put 3 and 3 as the factor pair. 3 is a prime number, so we underline both 3 and 3.
Now we have broken 1,800 into its factors, we need to gather up all the underlined factors because they are all prime numbers.
We have 5, 2, 2, 5, 2, 3 and 3
So, we can write that 1,800 as a product of prime factors is: 5 x 5 x 3 x 3 x 2 x 2 x 2 (Remember that product means to multiply)
We can also write this as 1,800 = 5² x 3² x 2³
Here is an example of a factor tree for the number 36, so that you can picture what they look like..
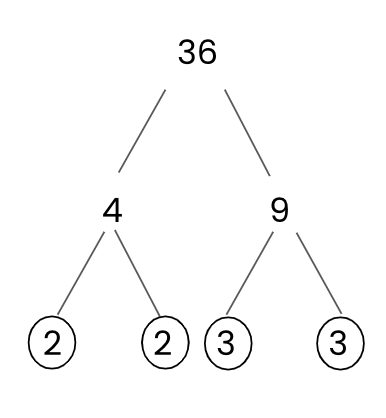
36 has been split into its factor pair of 4 and 9.
4 has been split into its factor pair of 2 and 2. Both are prime numbers, so they have been circled.
9 has been split into its factor pair of 3 and 3. Both are prime numbers, so they have been circled.
So, the prime factors of 36 are 2, 2, 3 and 3.
36 as a product of its prime factors is: 3 x 3 x 2 x 2 or 3² x 2²
Let's have a go at some questions now.
You can look back to this explanation at any time during the activity by clicking on the red button at the side of the screen.








