Identify Congruent Triangles

Triangles that are exactly the same shape and size are congruent.

Note: this also applies to shapes other than triangles.

Triangles are congruent for the following reasons:

Three matching sides (SSS)

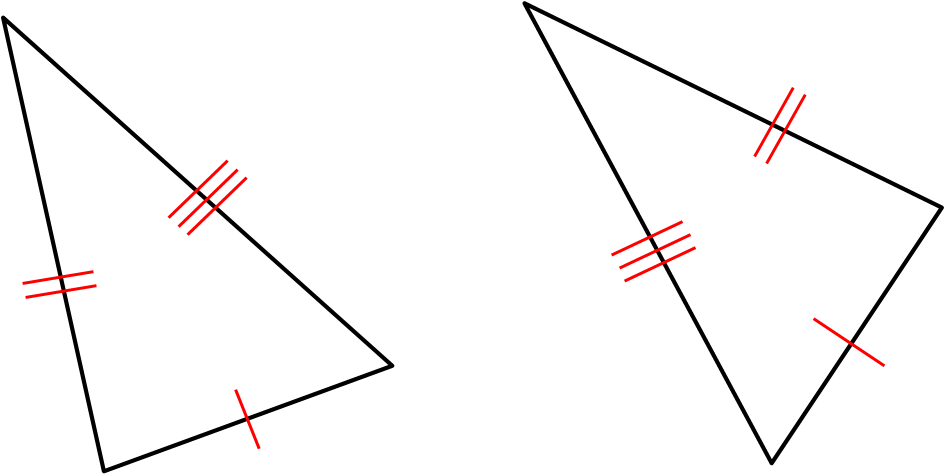
Two matching sides and the angle between them (SAS)

Two matching angles and a corresponding side (AAS)

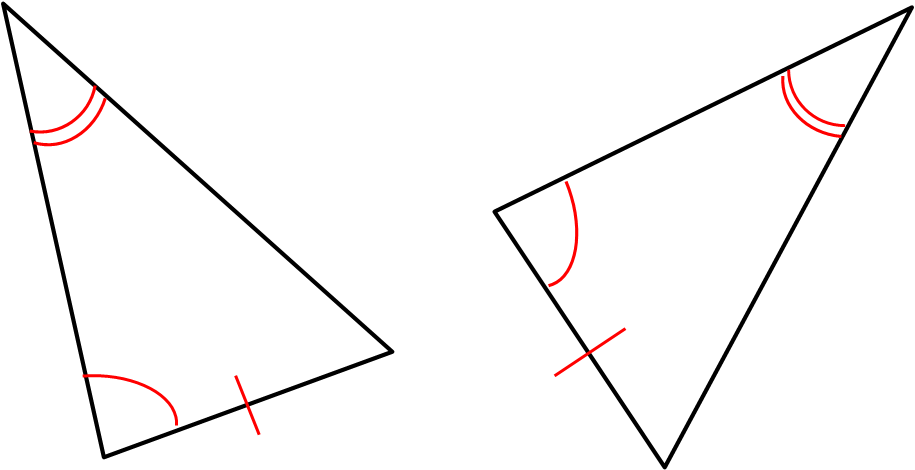
In a right-angled triangle, the hypotenuse and one matching side (RHS)

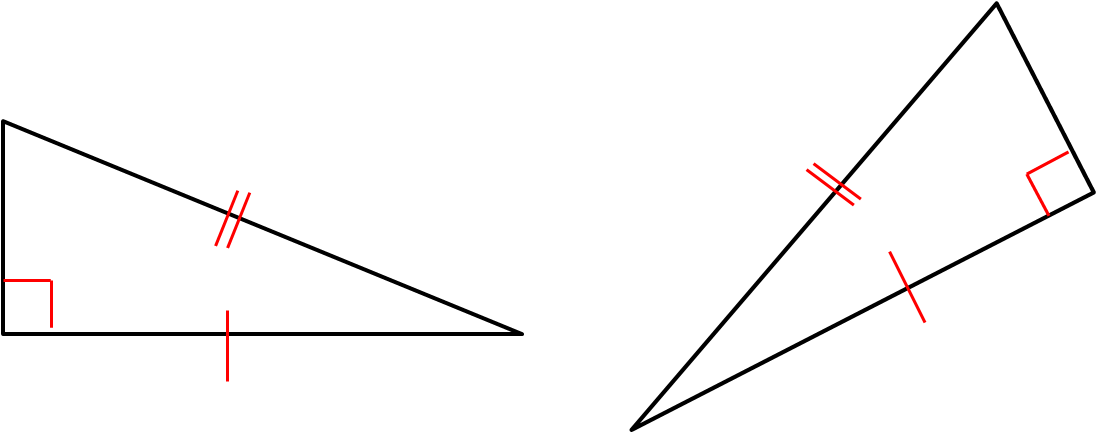
Now it's over to you. In this activity, we will identify congruent triangles and give reasons as to why they are in fact, congruent.