Find the Radius of a Sphere

The formula for the volume of a sphere, V, in terms of its radius, r, is:

V = 4/3 πr³

We can rearrange this formula to make r the subject.

If we multiply both sides by 3, we reach: 

3V = 4πr³

Then we can divide both sides by 4π to reach: 

r³ = 3V / 4π

Finally, we need to find the cubed root of both sides and the formula for the radius of a sphere, r, in terms of its volume, V, is:

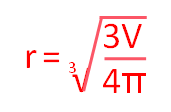
Example

Calculate the radius, r cm, of a sphere which has a volume of 100 cm³. 

Give your answer to 3 significant figures.

V = 4/3 πr³

100 = 4/3 πr³

Multiply both sides by 3: 300 = 4πr³

Divide both sides by 4π: 300 / 4π = r³

Find the cube root of this total: r = ^₃√ 300 / 4π

r = ^₃√23.873... = 2.8794... ≈ 2.88 cm (to 3 s.f.)

It looks complicated, but just take it one step at a time.

Let's give it a go!