Reflect in a Given Line

When you look in a mirror in the morning, what do you notice?

How far away from the mirror does your reflection appear to be?

 

It's the same distance from the mirror as you are.

If you get closer to the mirror, so does your reflection.

 

What happens if you raise your right hand?

 

Your reflection appears to raise it's left hand.

It's always the opposite way round.

 

In maths, we have to be able to use these observations when reflecting a shape.

 

 

What are the rules?

 

1) A reflection will be the same distance from the mirror line as the original object is;

2) Any reflected shape will appear the other way around.

 

 

 

Reflecting a point

 

e.g. Reflect point a in the y axis:

 

 

 

Step 1: Identify the mirror line and count how far away from it the point is:

 

The y axis is the main, vertical line through the centre of our grid.

We can then see that this is two squares away from the point we will reflect.

 

When we are counting to the mirror line, we always count at 90° to the line, like this:

 

 

 

Step 2: Count the same distance from the other side:

 

 

 

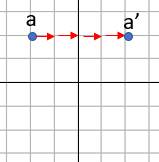
Step 3: Draw and label the new point:

 

When we are drawing reflections, we need to be able to tell which is the original, and which is the reflection.

To do this, we use an apostrophe to accompany the new point or image. 

 

If the original is a, the reflection is a':

 

 

 

 

 

Reflecting a shape

 

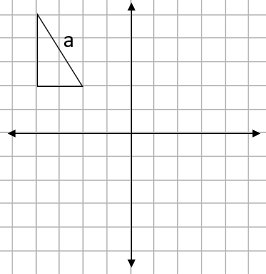
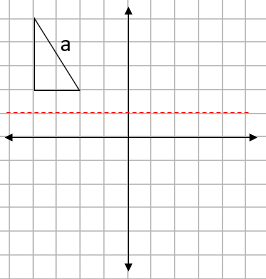
e.g. Reflect shape a in the line y = 1:

 

 

 

Step 1: Identify the mirror line:

 

Often, we will be asked to reflect in one of the axes.

In this question, we are asked to reflect in the line y = 1.

Remember that the line y = 1 will be a horizontal line that passes through the y axis at 1, like this:

 

 

 

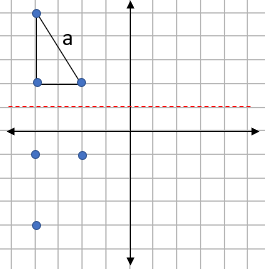
Step 2: Reflect each of the corner points (vertices) in the new mirror line:

 

We do this in the same way as we did with the single point above, but now we need to do it three times:

 

 

 

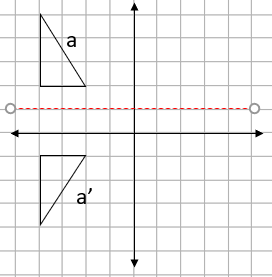
Step 3: Join up the points and label the shapes:

 

 

 

 

Let's give this a try now.

 

In this activity, we will reflect points and shapes in axes or defined lines applying the principles outlined above. 

 

You may find it helpful to have a pencil and some squared paper handy to support you in this activity. If you do not, you will need to be able to visualise these reflections in your mind's eye.