Being a weather forecaster is far more complex than just reading the weather on a map. To qualify as a weather forecaster, you need at least a degree in Science or Maths.
A vector is used to represent any quantity that has both magnitude and direction.
From working out how strong the wind will blow and in what direction it will be blowing, to calculating the rotation of a tornado, a forecaster will need to use vectors in their calculations.
This activity will introduce you to column vectors. This will show you how to represent vectors and write them correctly.
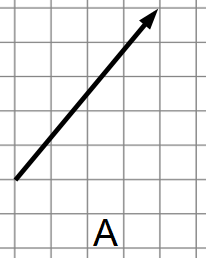
Example 1
An arrow is drawn on the grid. We can define this as a vector by counting the number of squares it moves across and up.
From its starting point to the tip of the arrow, this moves 4 squares forwards and 5 squares up.
To write this as a vector, we say:
The key point about column vectors is that they need to be in brackets, which can be either curved ( ) or square [ ].
The next thing to understand is that the top number shows how many squares the vector moves in the x-direction (forwards or backwards) and the bottom number shows how many squares it moves in the y-direction (up or down).
(Think of a co-ordinate grid with an x and y axis when we refer to the x-direction and y-direction).
Finally, don't mistake this for a fraction. There is no line between the two numbers and when you write a column vector in an exam, it would be incorrect to write it as [⅘].
Remember: it is simply two numbers arranged in a bracket to count the number of squares moved.
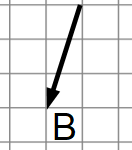
Example 2
This time, the arrow is pointing backwards and down.
We still count the squares in both directions, but we have to make the numbers negative.
The arrow has moved 1 square backwards and 3 squares down. This means as a column vector, we say:
Always make sure you put the numbers the right way round. Remember, the top number must be the x-direction and the bottom number must be the y-direction. To put them in the wrong order would send the arrow in a completely different direction.
Also keep an eye on whether your numbers are positive or negative, because it makes the difference between moving forwards and backwards, and up and down.
As we saw in Example 1, some vectors are entirely positive, and as we have just seen in Example 2, some entirely negative.
Some vectors may also contain one positive number and one negative number. Shown below is a summary of how to read a column vector:
Summary
Vector moves forwards: x-direction is positive
Vector moves backwards: x-direction is negative
Vector moves up: y-direction is positive
Vector moves down: y-direction is negative




![A = [4,5] in column vector](/userfiles/image/vector%20A%20%3D%204%2C5.PNG)