Do you ever play Battleships?
Did you ever find the treasure on that pirate map?
All great fun until you are asked to calculate midpoints of lines, their length or gradients.
So from Battleships to G.C.S.E questions, this is what we do:
Finding midpoints of lines
Example:
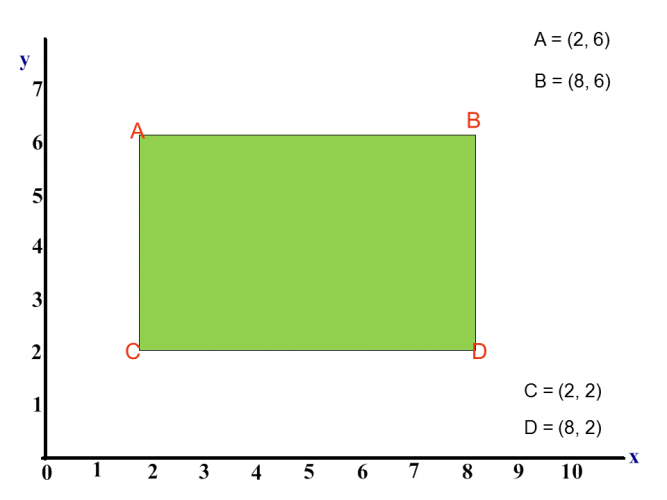
Find the midpoints of AB and BD
Midpoint of line AB:
Take both x coordinates and add 8 + 2 = 10. Now divide by 2 = 5
Take both y coordinates and add 6 + 6 = 12. Now divide by 2 = 6
Midpoint = (5,6)
Mid point of line BD:
Take both x coordinates and add 8 + 8 = 16. Now divide by 2 = 8
Take both y coordinates and add 6 + 2 = 8. Now divide by 2 = 4
Midpoint = (8,4)
You don't actually need a diagram, you can do this without:
Find the midpoint of AB. A = (2,7) B = (6,5)
2 + 6 = 8 ÷ 2 = 4
7 + 5 = 12 ÷ 2 = 6
Midpoint is (4,6)
Line Lengths
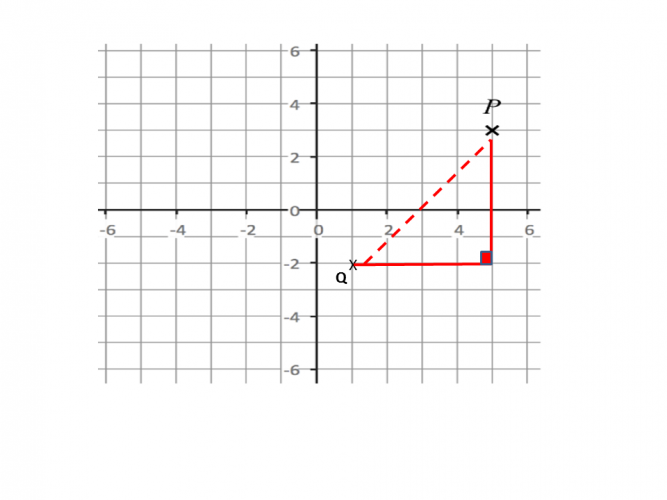
1. Write out the coordinates: P = (5,3) and Q = (1,-2)
On the diagram, you can see that these coordinates make a right-angled triangle.
2. Find the difference between the x coordinates.
The difference between x is 4 (5 - 1 = 4) and the difference between y is 5 (3 -- 2 is the same as 3 + 2 = 5)
3. Now apply Pythagoras's Theorem: a² + b² = c²
4² + 5² = √ 41
This is 6.4 units correct to 1 decimal place.
Gradients
Gradients are written in the form y = mx + c. The gradient is represented by the letter m.
Draw a right angle anywhere on the line. Count the units.
The gradient is rise ÷ run (vertical ÷ horizontal)
The vertical units = 5 and the horizontal units = 4
5 ÷ 4 = 1.25 units
Like the others, you can find a gradient without any diagram.
Find the gradient of the line with coordinate points A = (4,9) B = (6,13)
Here is the formula:
It just means take the second y coordinate and subtract the first y coordinate from it.
Do the same for the x coordinates and then divide.
13 - 9 = 4
6 - 4 = 2
4 ÷ 2 = 2
The gradient of the line is 2.

Let's get coordinated to find that treasure.