
Have you seen a footballer take a swerving free kick? By kicking the ball in just the right place they manage to curl it around the wall of defenders and into the back of the net.
The kick has direction and magnitude (size), the two properties required to describe vectors.
Do you think footballers are thinking about their maths lesson on vectors when they step up to take the free-kick? Probably not, they just want to score! But, they will be thinking about the direction and magnitude of the force they will kick the ball with.
Without even realising, footballers are using vector calculations every time they kick a ball!
Describing vectors
Vectors are often described using letters. They are represented with a labelled arrow between two points.
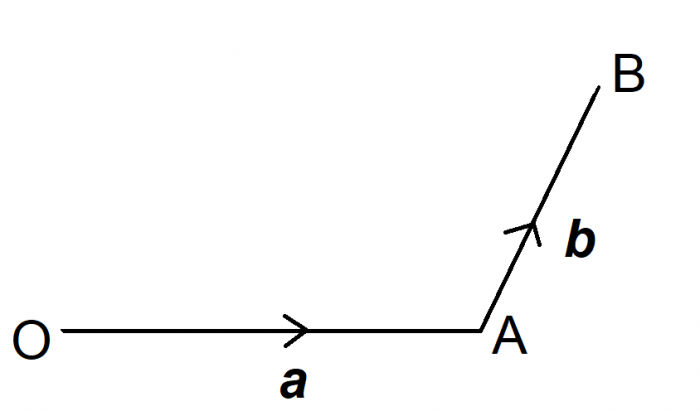
Two bold capital letters indicate a "route" between those two points. For example, OA means the route from O to A.
In this example, OA is described by vector a and AB is described by vector b.
An important rule to remember: If you want to "travel" in the opposite direction to your given vector, you must reverse the sign. For instance, we know that OA = a. Therefore, the opposite route, from A to O, ("AO") is defined as -a. This is a rule you may need to apply when combining vectors and writing them algebraically.
Joining vectors together
A typical GCSE exam question will present you with labelled vectors between various points, and then ask you to define a new vector between two of the points.
If you imagine the vectors as directions between two places, the way to join them together is to add them.
Let's look at an example and how to solve this type of question.
Example

OA = a
AB = b
There is no need to make anything negative, because the path you have taken is in the same direction as the given vectors.
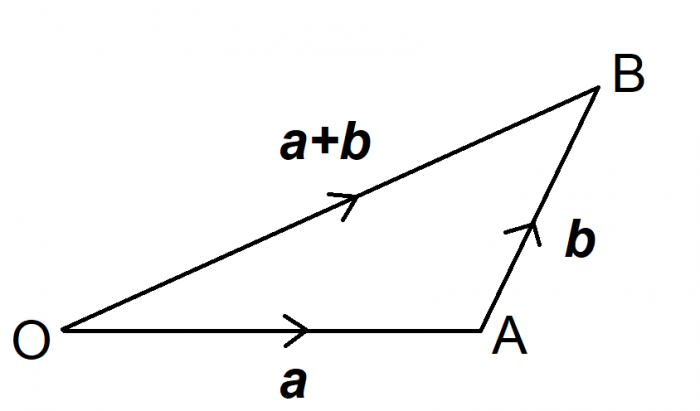
OB = a + b
Once you have defined your vector, you can apply the same logic and the same algebra to it as any other vector. For example, to find the midpoint of a vector, you simply halve it (i.e. the midpoint of OA = ½a). Therefore, using the same rule, the midpoint of OB = ½a + ½b.
Proving that two vectors are parallel
One last rule to be aware of: you can prove (or disprove) whether two vectors are parallel by showing whether or not they are multiples of each other.
For example, if you had the vector a+b, any multiple of this would be parallel to it. This would be a vector such as 2a+2b, 3a+3b, and so on.
This same proof can also be used for showing whether various points are on the same straight line.
Have a go at this activity and see if you can apply these rules.







