If you confident with positive integers, we are now going to learn to evaluate numbers using negative indices.
If you are not sure what these are, why not review these before you move forwards?
Think about the patterns you can see in the following table:
| Start with 1000 | 1000 | 10 x 10 x 10 | 103 |
| Then divide by 10 | 100 | 10 x 10 | 102 |
| Divide by 10 again | 10 | 10 | 101 |
| Divide by 10 again | 1 | 1 | 100 Remember that any term to the power of 0 is 1 |
| Divide by 10 again | .png) |
.png) |
10-1 |
| Divide by 10 again | .png) |
.png) |
10-2 |
| Divide by 10 again | .png) |
.png) |
10-3 |
We can see that the pattern in these powers of 10 shows us that:
.png)
Notice that we are, in fact, finding the 'reciprocal' of:
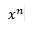
e.g. Evaluate 2-3.
This means work out the value of:
.png)
We have found the reciprocal of 23.
e.g. Evaluate 3-4.
This means work out the value of:
.png)
We have found the reciprocal of 34.
In this activity, we will evaluate and calculate negative indices with negative numbers and fractions as we have seen in the examples above.
You may want to have a pen and paper handy before you start so that you can compare your working to our answers written by a maths teacher.








