One of the skills you need to have to be successful in maths is being able to find the prime factors of any number.
This will enable you to solve complex problems in fewer steps and to speed up in your mental maths.
The proper name for this skill is finding or using 'the product of prime factors'.
Let's look at the meaning of each word:
Product: Numbers multiplied together.
Prime: A number that can only be divided by itself and 1 (e.g. 2, 3, 5, 7, 11, 13, 17, 19, etc.)
Factor: A number you can divide a target by that doesn't leave a remainder.
So if we are using the product of prime factor, we are breaking down a number into prime factors and writing them as a list that is then multiplied together.
e.g. We could write 8 as 2 x 2 x 2
This works because 2 is a factor of 8 but it is also a prime number, and we can use this number as a multiple to reach the target number.
How do we do this?
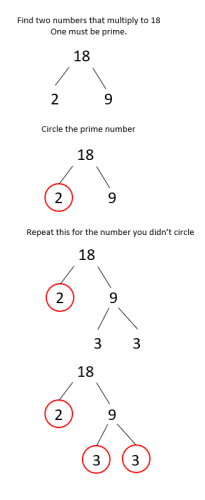
We use a technique called a prime factor tree.
e.g. Find the prime factors of 18.
Once we get to this point, we can write 18 as the product of its prime factors:
18 = 2 x 3 x 3
When we are writing these sums, we always write them in ascending order.
Writing in index form
Another skill we need is to write these answers in index form.
This sounds complicated, but it simply means to write them with powers.
So 18 = 2 x 3 x 3
Can also be written as:
18 = 2 x 32
Be careful if you are asked for index form; you can lose marks if you have the correct answer but miss this step or make an error at this late stage.
In this activity, you will find prime factors of numbers with up to three digits, recording them in both ascending lists and index form.
You will want to grab a pen and scrap paper before you start so you can draw your own prime factor trees.
Want a bit more help with this before you begin? Why not watch this short video?