When you first get introduced to the concept of finding the Highest Common Factor (HCF) and Lowest Common Multiple (LCM), you will probably have worked out answers by listing all the factors.
While this method is perfectly fine when you’re dealing with small numbers, it can get quite difficult if you have large numbers.
To find the HCF and LCM of large numbers, we need to tie together the topics of product of prime factors and Venn diagrams.
e.g. Find the HCF and LCM of 140 and 120.
Step 1: Find the product of prime factors for both numbers.
(If you’re unsure of how to do this, it would be useful to complete an activity to revise this skill first.)
Our prime factor trees for both numbers will look like this:
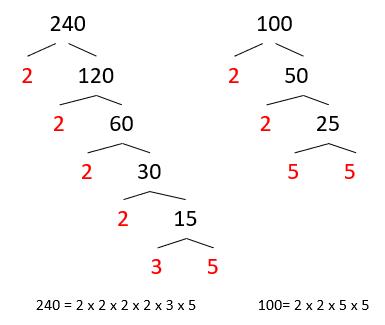
Step 2: Identify the numbers which appear in both lists.
240 = 2 x 2 x 2 x 2 x 3 x 5
100 = 2 x 2 x 5 x 5
Step 3: Put these overlapping numbers into the centre of a Venn diagram.
Note that we only put each number in once.
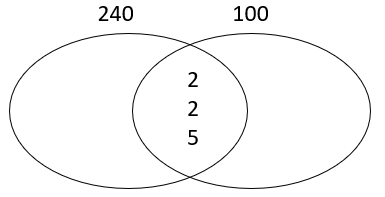
Step 4: Put the other numbers from the prime factor trees into the Venn diagram:
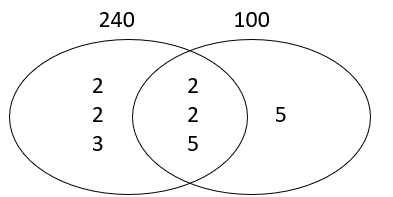
Step 5: Identify the HCF and LCM.
The HCF can be found by multiplying together all the numbers in the overlap:
2 x 2 x 5 = 20
The LCM can be found by multiplying together all the numbers inside the Venn diagram:
2 x 2 x 3 x 2 x 2 x 5 x 5 = 1200
In this activity, you will find the HCFs and LCMs of larger numbers (with two or three digits) which would be very challenging to calculate using lists.
You will need to have a pen and paper handy so that you can create your own Venn diagrams as you work.
Want a bit more help with this before you begin? Why not watch this short video?








