When we find calculate areas and circumferences of circles, or when we use the formula for the volume of a cylinder or a sphere, we work with pi ( written 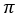 ).
).

If you work this out on your calculator, the first answer you see looks like this:

So we are shown an answer as a multiple of pi, rather than a number with decimal places.
If we are asked to find an exact value for the circumference of this circle the answer is 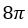 cm.
cm.
We would say the answer verbally as "eight pi cms".
This means we have 8 "lots of" pi in our exact answer.
Notice that as we are expressing this using algebra, we don't use the multiplication sign (to avoid confusing it with the letter 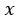 ).
).
If we need to find the exact area of this circle we would calculate the following:
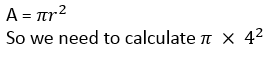
The calculator gives us this answer (which is an exact answer) as a multiple of pi too:
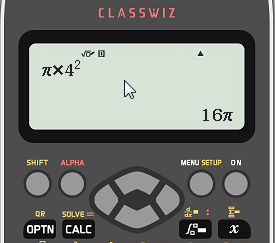
We would say that the exact area of this circle is "sixteen pi cm squared".
We can also work out these calculations mentally by multiplying (or squaring) the numbers involved in the calculations and then using this result as our multiple of pi (with correct units):
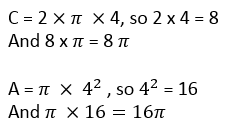
Let's try some questions now to put these formulae into practise.
Try to work out the answers without a calculator, as these types of calculations can be asked on a non-calculator exam, which will mean expressing your answer in terms of π.
Remember to always give the correct units with your answers.








