Have you ever wondered why your calculator seems to prefer answers in fraction form wherever possible?
For example, here we have given the calculator 2 decimal numbers to multiply, but it has given us the answer in fractions first:

This is because the calculator is giving us this rational number in the simplest form possible.
A rational number is a number that can be expressed using a ratio (i.e. fraction), in the form:
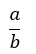 where a and b are integers or whole numbers
where a and b are integers or whole numbers
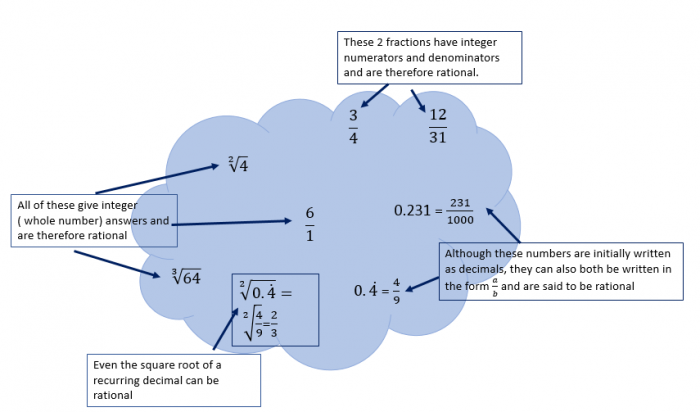
Here are some examples of rational numbers:
However, not all numbers can be written in this form.
Any number that cannot be written in this form is called irrational.
If we ask our calculator to work out a square root, e.g.
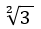 = 3.46410161514... or
= 3.46410161514... or 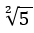 = 4.472135955...
= 4.472135955...
If we think of Pi, this is an irrational number as it just keeps on going! Our calculators may record it as 3.14159265359, but we know that this is only a small section of this infinite number!
These answers do not terminate and so cannot be written in the form:
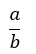
Remember that a number written under a root sign is called a surd.
These numbers are said to be irrational, as they do not terminate once calculated.
Other examples of irrational numbers include some cube and higher roots, plus other numbers expressed as symbols in addition to π.
In this activity, we will identify if numbers are rational or irrational and use this knowledge to help us solve problems.







