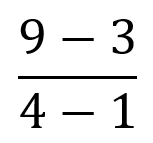The gradient of a line is a number defining its steepness.
We can find this by using the coordinates of two points.
If the first point has coordinates (xa, ya) and the second has coordinates (xb, yb), we can use the formula below to find the value of the gradient:
Let's have a look at an example to see this in action.
e.g. Find the gradient of a line passing through (1, 3) and (4, 9).
The formula above means that we need to subtract the y-coordinates of both points, then subtract the x-coordinates and divide the former by the latter.
We can do this in stages or in one go using a calculator.
In stages:
9 - 3 = 6
4 - 1 = 3
6 ÷ 3 = 2
So the gradient is 2.
Using a calculator:
This is what we need to put into our calculator:
So the gradient is 2.
In this activity, we will find the gradients of straight lines when given the coordinates of two points on the line.
If you prefer the second method in the options above, you may want to have a calculator handy to support you.
Want a bit more help with this before you begin? Why not watch this short video?