Identify Transformations with Trigonometric Graphs

There are six transformations that you can perform on the graph of a function.

Let’s look at what happens when we apply these to the function y = sin (x) 0 ≤ x ≤ 360

The results will be the same for the functions y = cos (x) and y = tan (x).

 

f(x) → f(x) + a     {Translation with a vector of  }

 

 

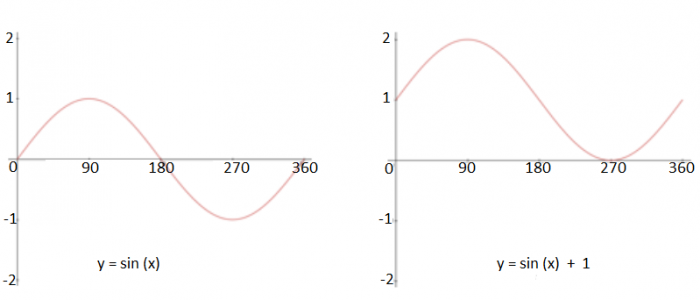
Sin (x) → sin (x) + 1 has the effect of moving the graph upwards by 1.    

 

f(x) → f(x + a)     {Translation with a vector of }

 

 

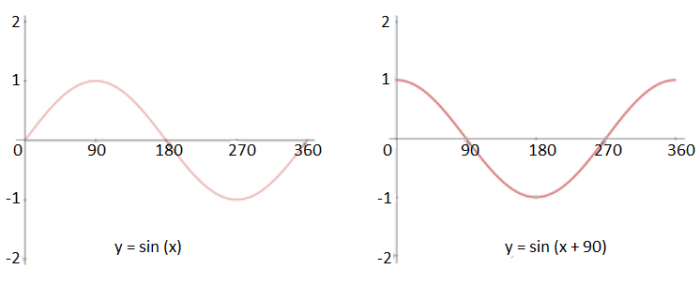
Sin (x) → sin (x + 90) has the effect of moving the graph left by 90°.

This transforms y = sin(x) into y = cos(x).

 

f(x) → af(x)         {Stretch in the y-axis, scale factor a}

 

 

Sin (x) → 2sin (x) has the effect of increasing every value of y by 2. It stretches the graph vertically.

 

f(x) → f(ax)         {Stretch in the x-axis, scale factor 1/a}

 

 

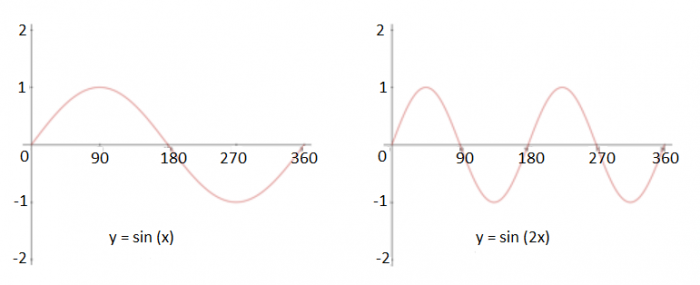
Sin (x) → sin (2x) has the effect of multiplying every value of x by 1/2. It compresses the graph horizontally.

 

f(x) → -f(x)          {Reflection in the x-axis }

 

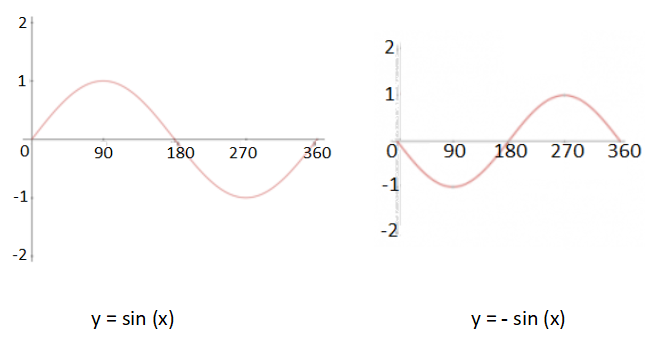
Sin (x) → -sin (x) has the effect of reflecting the entire graph in the x-axis.

 

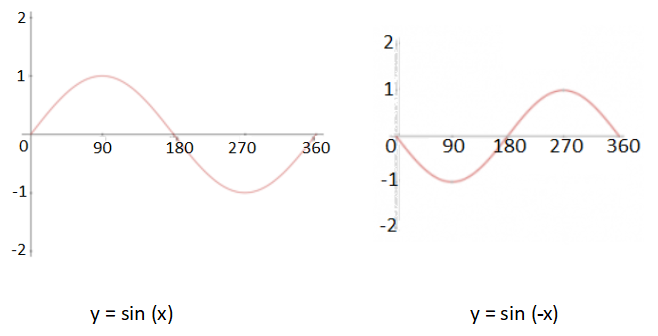
f(x) → f(-x)          {Reflection in the y-axis}

 

 

Sin (x) → sin (-x) has the effect of reflecting the entire graph in the y-axis.

In the case of transforming sin (x), you have probably noticed that sin (-x) = - sin(x).    

Now it's time for some questions!