EdPlace's GCSE Home Learning Maths Lesson: Calculate and Interpret Gradients
Looking for short lessons to keep your child engaged and learning? Our experienced team of teachers have created English, maths and science lessons for the home, so your child can learn no matter where they are. And, as all activities are self-marked, you really can encourage your child to be an independent learner.
Get them started on the lesson below and then jump into our teacher-created activities to practice what they've learnt. We've recommended five to ensure they feel secure in their knowledge - 5-a-day helps keeps the learning loss at bay (or so we think!). Are they keen to start practising straight away? Head to the bottom of the page to find the activities.
Now...onto the lesson!
Why Does Your Child Need to Master Gradients?
Gradients are a common topic in Key Stage 3 and having a solid understanding is useful for both maths and science. Students will have been exposed to line graphs already, but now they need to understand the logic behind a gradient on a graph. This knowledge will allow them to calculate gradients using either coordinates or measurements.
We're confident that by following this step-by-step guide your child will be able to:
1) Recognise a gradient as positive or negative
2) Calculate a gradient by making the correct measurements on a graph
3) Calculate a gradient using two sets of coordinates
Step 1 - What is a Gradient?
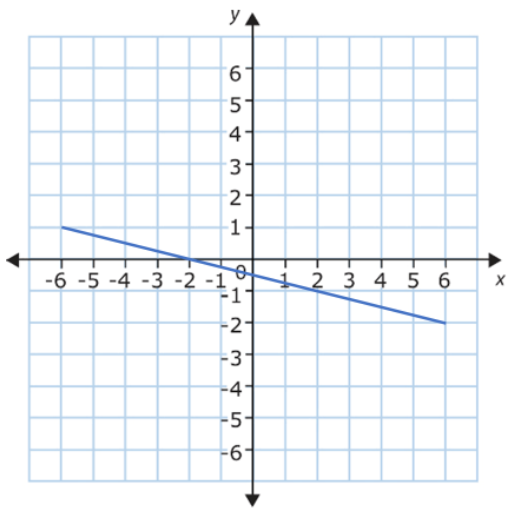
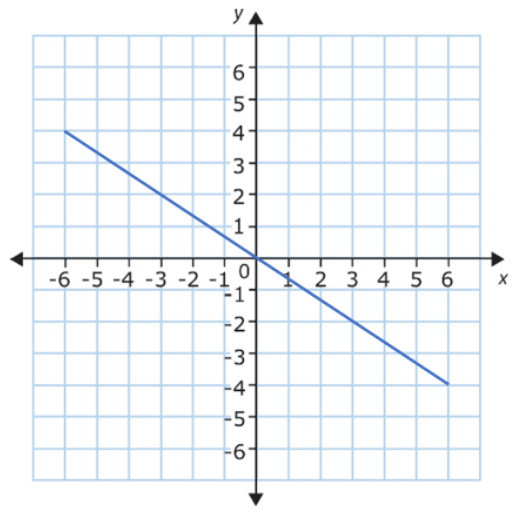
Before we learn how to calculate a gradient your child needs to understand what a gradient is. A gradient is just a number that tells us the steepness of a line. It can be positive, negative, or zero. Some simple illustrations will demonstrate this:
Shallow line = low gradient Steep line = high gradient
Downwards line = negative gradient Horizontal line = no gradient
Step 2 - How To Calculate a Gradient From a Graph
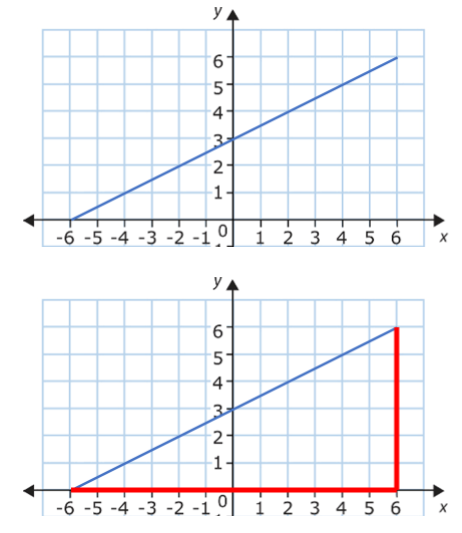
Now, we will start to look at how to calculate a gradient from a graph. The first thing to do is draw two straight lines to turn your line into a right-angled triangle. For example, to find the gradient of this line, we draw the two red lines as shown:
An important point is that it does not matter how big you make the triangle. It will not affect the final answer. However, it is a good idea to make the triangle as large as possible and to make life easier, use a whole number of squares.
Step 3 - Draw a Triangle then Apply the Equation
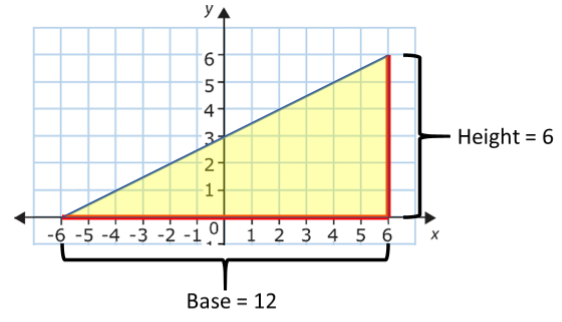
The thing to do now is to measure the height and base of this triangle. A common mistake that students make is just measuring the lines in centimetres with a ruler, this will give incorrect numbers if the scale of the axes is not in cm. Always use the numbers on the axes to work out the lengths. It really is as simple as counting squares.
In this case:
It is time to introduce the equation.
The equation of gradient is:
It looks complicated, but it just means “change in y co-ordinates divided by change in x co-ordinates”.
In other words, it's just the height of the triangle ÷ base of the triangle.
So, the gradient of this line is 1/2.
So, finding a gradient is as simple as drawing a right-angled triangle and dividing the height by the base. One last handy shortcut is knowing that you don’t even need to have the graph in front of you to find the gradient.
As gradient is “change in y co-ordinates divided by change in x co-ordinates”, we just need two pairs of coordinates. For example, an exam question may just say:
Find the gradient of a line that passes through (1,3) and (3,15)
Look at the y co-ordinates: 3 to 15 is a change of 12.
Look at the x co-ordinates: 1 to 3 is a change of 2.
Gradient = change in y ÷ change in x = 12 ÷ 2 = 6.
So, this gradient is 6. Simple!
Step 4 - Practice Questions
Using steps 1-3, see if your child can now work out these gradients:
a)
b)
c)
d)
Step 5 - Give it a Go...
Now that you’ve learnt to simplify algebraic fractions, see if your child can apply their knowledge to the following 5 activities. Have them complete them in the order listed below. All activities are created by teachers and automatically marked.
Plus, with an EdPlace subscription, we can automatically progress your child at a level that's right for them. Sending you progress reports along the way so you can track and measure progress, together - brilliant!
Activity 1 - Calculate the Gradient of a Line
Activity 2 - Calculate the Gradient of a Line Given Two Points
Activity 3 - Find the Gradient Between Two Points
Activity 4 - Find the Coordinates of the Midpoint of a Line Segment
Activity 5 - Find the Equation of a Line
Answers
a)
b)
c)
d)
Keep going! Looking for more activities, different subjects or year groups?
Click the button below to view the EdPlace English, maths, science and 11+ activity library

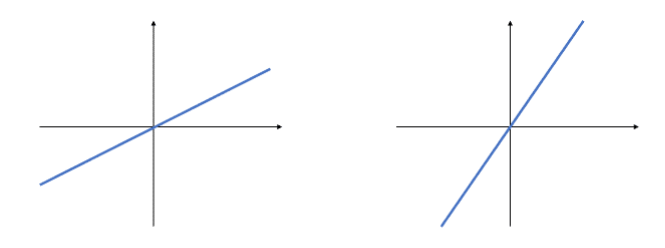
.PNG)