A cylinder can be considered as lots of circular discs stacked one above the other.

If the area of each circular disc is A and the height of the stack is h, then the volume = Ah.
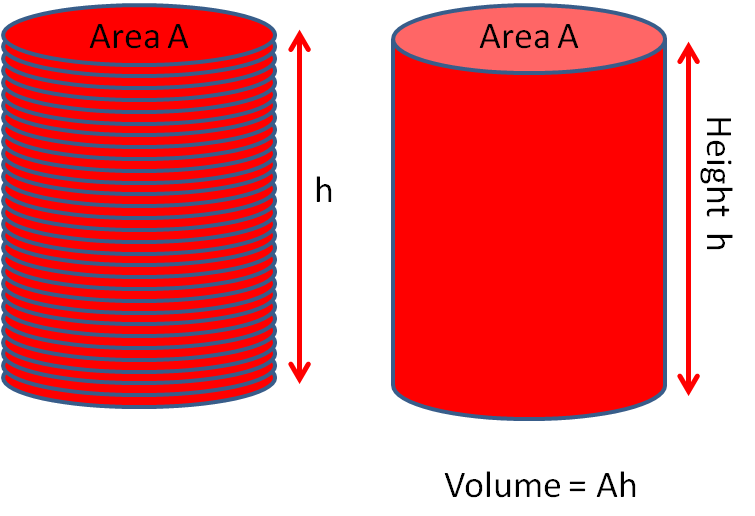
Remember that the area of a circle is πr2 where r is the radius of the circle.
So the volume of a cylinder with radius r and height h = π x r2 x h or as πr2h
Example
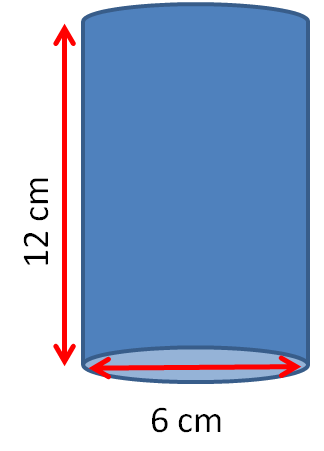
Find the volume of this cylinder in cm3 to 3 significant figures.
Answer
Diameter = 6 cm
Radius = 6 ÷ 2 = 3 cm
Height = 12 cm
Volume = πr2h = π × 32 × 12 = π x 9 x 12 = 339.29 ≈ 339 cm3 (3 s.f.)
Let's try some questions now.








