Many surds can be simplified using square factors.
You may have met these rules for surds:
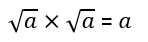
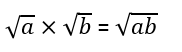
Let's look at an example now.
Using these rules means that we can write:
e.g. 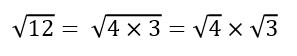
We can now take this one step further:
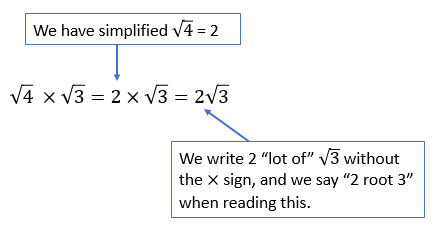
We will need to look for square factors of any surd we are asked to simplify.
Here is another example.
e.g. Simplify:
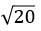
We need to think about the factors of 20.
They are 1 x 20, 2 x 10 and 4 x 5.
We know that 4 is a square number and so it would be helpful to rewrite √20 as 4 x 5.
So we can simplify as follows:
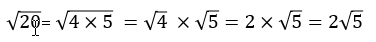
In this activity, we will simplify surds into multiples of square roots.
This will be a useful skill to support your mental maths and problem solving in all areas of maths.
You may want to have a pen and paper handy so that you can record your working and compare these to our examples written by a teacher.







