Recognise and Interpret Quadratic Graphs

Over the years, you will have dealt in quite a lot of detail with linear graphs.

This activity will look at the concept of the quadratic graph.

While you have to be able to do all sorts of things with quadratic graphs, this activity will concentrate on what they look like, identifying them and naming the significant points.

 

What is a quadratic graph?

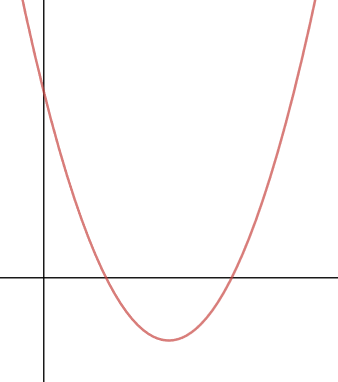
A quadratic is any graph that has the highest power in the function of x².

For example:  y = x² – 4x + 1 is a quadratic function.

You can quite easily spot a quadratic function as it has a very specific shape.

It is a smooth curve with one turning point which means it changes direction!

 

 

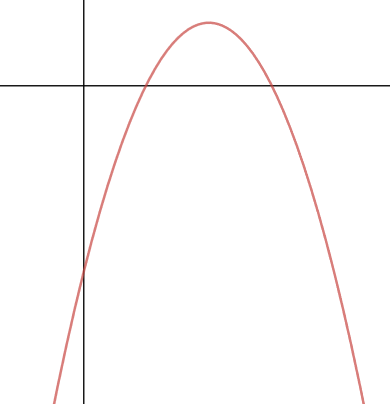
The negative quadratic

Quite frequently, you are expected to be able to sort quadratics that are upside down!

If you get one of these, the key thing to remember is that the function will start with -x² (spot that cheeky little minus sign)

 

 

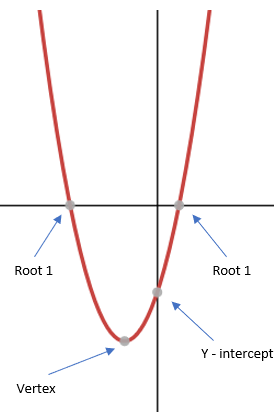
The significant points of the quadratic graph

There are three types of significant points on a quadratic graph -  roots/solutions, the turning point (also called the vertex) and the y–intercept.

 

These can be found at the following places:

 

 

Now it's time for some questions.