So far, you will probably have dealt in quite a lot of detail with linear, quadratic and circular graphs.
There are a few more graphs you have to be able to deal with.
This activity looks at cubics and reciprocals.
The good news with these is that you only have to be able to recognise, sketch and categorise these graphs and their function.
What is a cubic graph?
A cubic is any graph that has the highest power in the function of x3.
For example: y = x3 + x2 – 4x + 1 is a cubic function.
You can quite easily spot a cubic function as it has a very specific shape. It is a curve with two turning points, meaning that it changes direction twice.
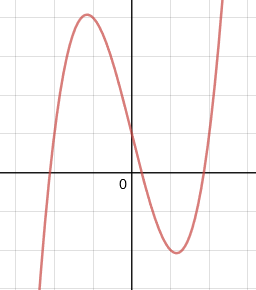
The negative cubic
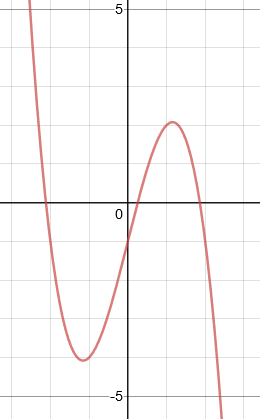
Quite frequently, you are expected to be able to spot cubics that are of the form y = -x3
The only difference here is that the graph will be the other way round. Instead of starting at the bottom and going up initially, it will start at the top and come down.
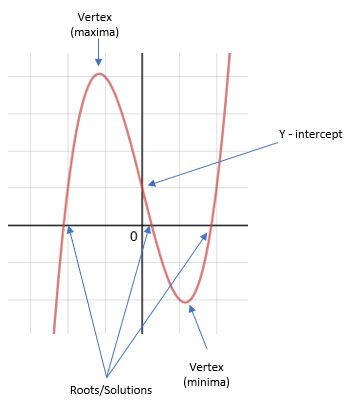
The significant points of the cubic graph
There are three types of significant point on a cubic graph - roots/solutions, turning points (also called vertices) and the y-intercept.
These can be found at the following points:
What is a reciprocal graph?
A reciprocal is any graph that has the general form y = 1/x
For example: y = 2/x is a reciprocal function.
Reciprocal functions have a very specific shape. You are, as with the cubic, expected to be able to recognise both positive and negative reciprocal graphs.
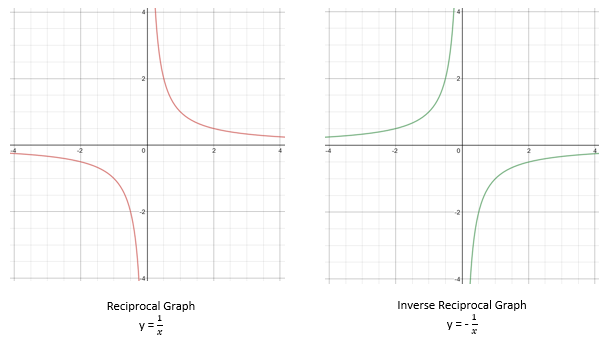
The significant points of the reciprocal graph
You can probably see from the graph that the curve seems to be straightening out when it gets nearer to the axis.
In fact, these get closer and closer to the axes but never touch them. This is called an asymptote.
Let's move on to the questions now.








