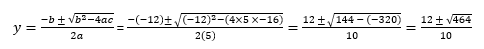If you are aiming for the highest possible grades in GCSE maths, you need to be looking consistently at the 5/6 mark questions at the end of the paper.
One of the topics that frequently appears in this position is solving linear and non-linear simultaneous equations.
To solve non-linear simultaneous equations, you cannot use the elimination method as this only works for linear functions. Instead, you have to use the quadratic formula.
Example:
Solve the following simultaneous equations:
x2 + y2 = 25
x + 2y = 3
Give your answers to 3 significant figures.
Step 1: Rearrange one of the equations into the form x = or y =
It doesn’t actually matter which one you do here, but there are a couple of guidelines:
Always rearrange the linear expression.
Try to avoid fractions.
Because of these rules, you need to rearrange the linear equation into the form x = 3 – 2y
Step 2: Substitute this rearranged equation into the non-linear equation.
x2 + y2 = 25 → (3 - 2y)2 + y2 = 25
The reason behind this is that we now have an equation that only has one variable (y) that we can solve.
Step 3: Expand and rearrange.
We can see that the equation (3 - 2y)2 + y2 = 25 is a quadratic, so we need to rearrange it into the form ay2 + by + c = 0
(3 - 2y)2 + y2 = 25
(3 – 2y)(3 – 2y) + y2 = 25
9 – 12y + 4y2 + y2 = 25
5y2 – 12y + 9 = 25
5y2 – 12y - 16 = 0
Step 4: Solve the quadratic to find the values of y.
Sometimes we can factorise this but for this example, you are asked to give your answers to 3 significant figures. This means you have to use the quadratic formula.
Evaluating this gives the values: y1 = 3.35 and y2 = -0.954
Step 5: Use the value of y to find the values of x.
All we have to do to find the values of x is to substitute our values of y into the rearranged linear equation.
x1 = 3 – 2(y1) = 3 – 2(3.35) = -3.71
x2 = 3 – 2(y2) = 3 – 2(-0.954) = 4.91
So the solutions to our two simultaneous equations are (-3.71,3.35) and (4.91,-0.954)
Time for some questions.