All cars have a speedometer, used to measure the speed of the car. In the UK, our speedometers measure speed in miles per hour (mph).
There is an example of a speedometer in the image below. However, this speedometer measures speed in kilometres per hour (km/h).

In fact, only about 9% of the countries in the world use miles per hour for measuring speed and setting speed limits on roads, the rest of the countries use kilometres per hour. Miles per hour and kilometres per hour are examples of units that we measure speed in, but there are lots of other units that people use too, in different situations.
Let's review how to calculate speed, and some of the common units for speed!

Speed is a word we use to describe how fast something moves. The greater the speed, the faster something is moving.
Speed can be calculated using this equation:
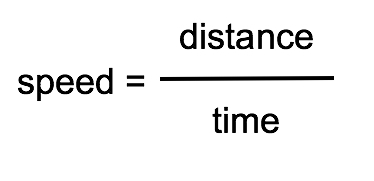
At the start of this introduction, we said that one common unit to measure speed is miles per hour. Let's look at an example of how to use that unit with this equation.
Example
A car travels 60 miles in 2 hours. What is the speed of the car?

Answer
If we remember the equation for speed, we can solve this by calculating the distance the car travels, divided by time.
60 miles divided by 2 hours is 30, so the answer is 30 miles per hour, or 30 mph.
As we said at the start of this activity, there are lots of units that people use to measure speed! If you were in France, the speed limits on the roads would all be in kilometres per hour.
If you were sailing a boat, you might measure the speed of the boat in knots (nautical miles per hour).
For objects that move more slowly, a common unit would be metres per second (m/s). This unit is known as the standard unit for speed, and is used most often in science and engineering.
You might have noticed that the units for speed all follow a similar format - a distance per time period, like metres per second or kilometres per hour. This is because the unit of speed is based on the equation for speed that we saw earlier - a distance divided by a time.
Let's look at one more example.
Example
A student runs 30 metres in 20 seconds. What is their speed, and what is the right unit?

Answer
If we remember the equation for speed, we can solve this by calculating the distance the student travels, divided by time.
30 metres divided by 20 seconds is 1.5.
So, the answer is 1.5 m/s because the distance was measured in metres, and the time was measured in seconds.
Well done! Now, let's try some questions to check our understanding.








