The speed of a chemical reaction makes a big difference to its effects. Fireworks involve metals reacting with oxygen in a fraction of a second...

... but rusting happens over a period of years, despite also involving a metal and oxygen.

We can describe this difference by using an aspect of particle behaviour called collision theory to explain why some reactions are fast and some are slow.
This helps people to make good reactions (such as pretty fireworks) go faster, and make bad reactions (such as rusting) go more slowly.
Rates of reaction
Suppose we start a chemical reaction and record how much product is made over time. Unless something very strange happens, the graph will look like this:
.jpg)
The first part of the graph is a straight line - this is also the time when the reaction is fastest. As time passes, the reaction starts to go more slowly, then it stops. This is called completion - for the reaction in the graph, completion is at about 10 - 12 minutes.
The amount of product made doesn't depend on the rate of reaction - it is fixed by the amounts of reactant put into the reaction.
The reaction rate tells us how quickly the reaction happens.
To work out the rate of reaction, we calculate:
rate of reaction = amount of product ÷ time taken
For example, in the graph, the first two minutes of the graph are pretty much a straight line. In that time, the reaction makes 9 cm3 gas, so:
The initial rate of reaction = 9 cm3 ÷ 2 min = 4.5 cm3 / min.
Since 2 min = 120 s, we could also write this as: initial rate of reaction = 9 cm3 ÷ 120 s = 0.075 cm3 / s.
As the reaction progresses, the rate of reaction slows down. The graph shows this by becoming less steep.
A better way to use the graph (and the only way that works when the graph is noticeably curved) is to draw the tangent to the graph at the moment of interest. So let's take another graph.
What is the rate for this reaction at t = 40 seconds?
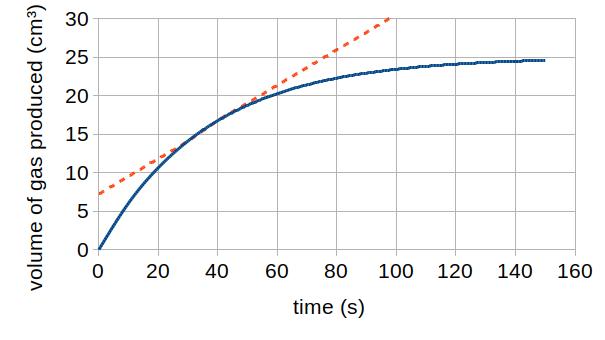
The red dotted line is the tangent to the graph at x = 40 seconds - it's a straight line which touches the graph at 40 seconds, without cutting it.
The gradient of the graph at that moment is the same as the gradient of the tangent. But since the tangent is a straight line, we can work out its gradient using up ÷ across.
Just remember that in science graphs, the up and across numbers need to relate to the numbers on the axes - you can't just count squares.
The tangent line goes from 7 cm3 at t = 0 s to 30 cm3 at t = 95 s. So the up is 30 - 7 = 23 cm3, and the across = 95 - 0 = 95 s. This means that the gradient of the tangent = 23 ÷ 95 = 0.24 cm3 / s.
So, the rate of reaction at 40 s = 0.24 cm3 / s.
Collision theory
There are several factors which change the rate of reaction. One big idea links them all - collision theory.
For two particles to react, they have to collide in the right orientation and with enough energy to break the atomic bonds in the particles.
The more frequently these collisions happen, the faster the rate of reaction will be.
Once we understand collision theory, we can explain why some reactions are fast and some are slow. We can also speed up or slow down reactions if that is what we need to do.
To speed up a reaction, we just need to make useful collisions happen more frequently.
Now let's move on to some questions.







