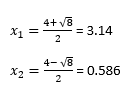Use the Quadratic Formula

One of the most common topics that you will come across in a GCSE higher maths exam is solving quadratics.

There are a number of methods you can use: factorising is one and completing the square is another.

However, both of these methods have the weakness that they don’t always work.

If a quadratic can be solved, the quadratic formula always works.

 

What is the quadratic formula?

On the old specification, you were given the quadratic formula. On the new specification, you are expected to recall it (so get learning):

 

 

To use the formula, all you have to do is work out the values of a, b and c,  plug them into the formula and evaluate it.

 

How do I know when to use the formula?

There is a very easy way to spot this.

On a calculator paper, it will say ‘Give your answers to 3sf.'

On a non-calculator paper, it will say ‘Give you answers in surd form.’

 

Example 1:

Solve x² – 4x + 2, give your answers to 3sf.

 

Step 1: Identify a, b and c

From the equation x² – 4x + 2 = 0 → a = 1, b = -4 and c = 2

 

Step 2: Plug this into the formula

 

 

When you look at this, make sure you keep the brackets - this makes sure that you won’t make a mistake with your signs.

 

Step 3: Simplify the formula

 

 

 

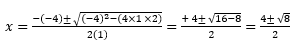
Step 4: Evaluate the two expressions

You should notice that the sign ± is in the quadratic formula. All this means is that there are two solutions - one given by the plus and one by the minus.

 

 

Example 2:

Solve x² – 4x + 2, give your answers as surds in their simplest form.

The method behind this is exactly the same as shown above until the end of step 3.

 

 

 

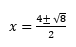
While this would get you some marks, to get full points, you would need to simplify the surds and cancel if it is possible:

√8 = √4 x √2 = 2√2

 

 

 

Next, if we cancel a factor of 2 from all the terms, we get: x = 2 ± √2

 

Let's try some questions now.