Describe Velocity and Calculate Relative Motion

Relative motion is all about motion in relation to a frame of reference. A frame of reference is the motion of an observer of the motion of an object.

 

Imagine you are sitting by your window observing a car driving past your house. From your perspective, you are at rest and the car is moving. However, from the point of view of a passenger in the car, they are sitting still and they would see you (along with your house and all the surroundings) as moving. You and the passenger have a different frame of reference.

 

Let's think of a different situation. An observer at a train station sees a fast train zoom past them at a speed of 100 mph. If the observer could see inside the train, a cup of coffee in a passenger's hand would be seen as moving at the same speed as the train. On the other hand, a passenger sat on that train would perceive the same cup of coffee being at rest in their hand. 

 

From the point of view of the passenger, the coffee cup is stationary. From the point of view of the person on the platform, the cup is moving at 100 mph! The two people have different frames of reference, so they observe the speed differently.

 

Calculating relative motion

Imagine a ball was thrown on a moving train. The ball is thrown at 5 m/s and the train is moving at 10 m/s. As you are probably starting to work out, if you asked the question "How fast is the ball moving?", it depends on your frame of reference. Its speed would appear different to the people on the train, compared to someone looking at the train from the platform.

 

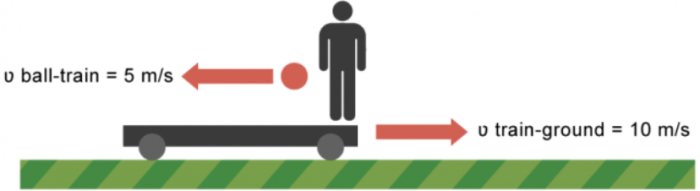
Let's make this clearer. Look at the diagram of a train floor and a ball. The speed of the ball with respect to the train is 5 m/s. The speed of the train with respect to the ground is 10 m/s. 

 

 

 

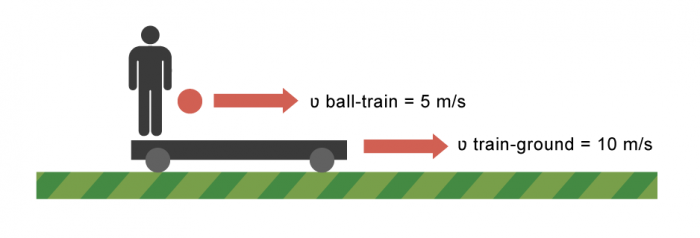
So if someone outside the train is watching the ball moving, they will see it moving at 15 m/s, which is the sum of the speed of the train and the speed of the ball (with respect to the train). In other words, when the frame of reference and the motion of the object are moving in the same direction, we add them to find the relative speed.

(10 m/s + 5 m/s = 15 m/s)

 

Now imagine the ball was thrown in the opposite direction. The observer on the platform would actually see the ball slowing down - and maybe even move to the opposite direction - depending on the speed of the train and the speed the ball was thrown at. This is because speed is not only a number, but a vector, called velocity. A vector is represented by an arrow, the length of which indicates the size of the speed, whereas the direction the arrow points towards indicates the direction of movement.

 

Let's keep the numbers the same: 

 

 

To the people on the train, the ball is moving at 5 m/s to the left. However, to an observer on the platform, it is moving at 5 m/s to the right. This is because the frame of reference and the object are moving in opposite directions, so we must subtract their speeds.

 

(10 m/s - 5 m/s = 5 m/s)

 

As long as you can recall the rule that moving in the same direction means we add, and moving in the opposite direction means we subtract, you can solve problems on frames of reference.

 

We will now explore relative motion further through the questions that follow.