Apply Congruence Rules

Today I saw twin pandas... that BEARS repeating!

 

 

Also, I found out I had a TWIN sister... I am beside myself!

 

Oh come on, what better way to introduce the topic of congruency than with a few jokes?

 

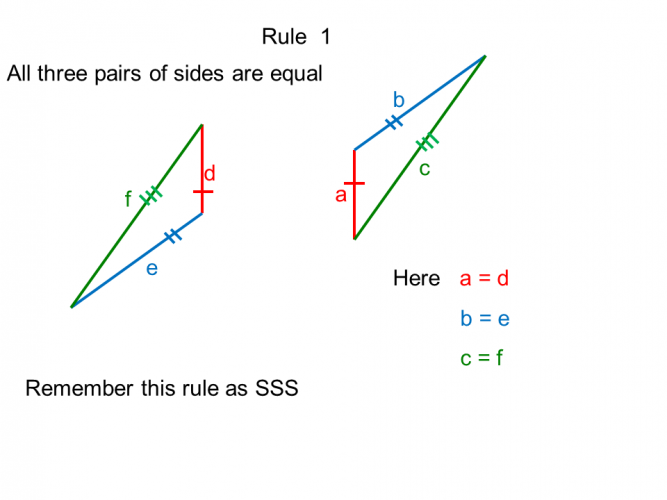
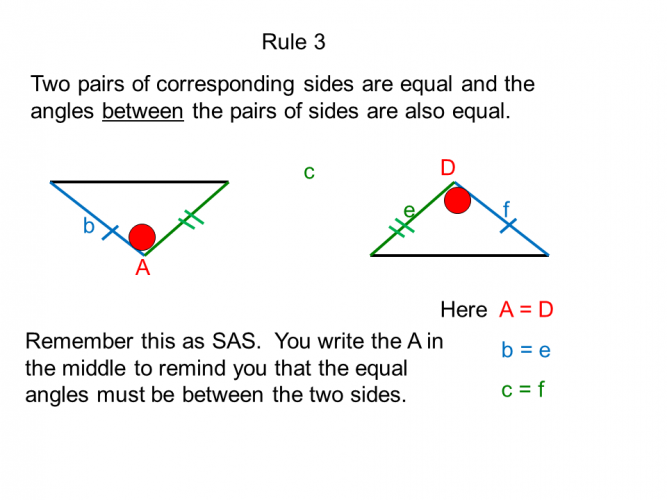
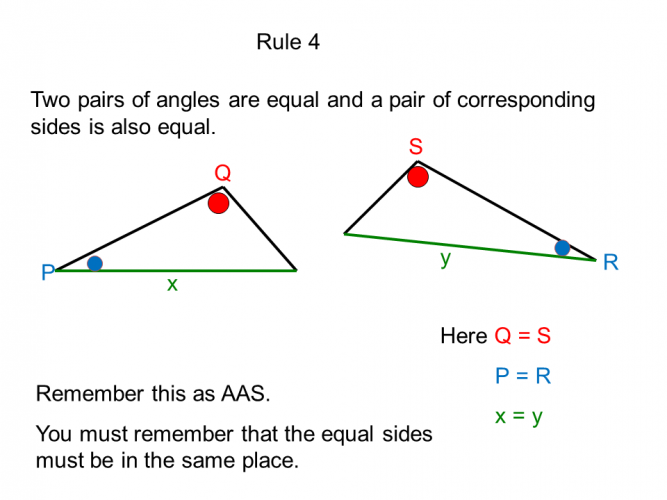
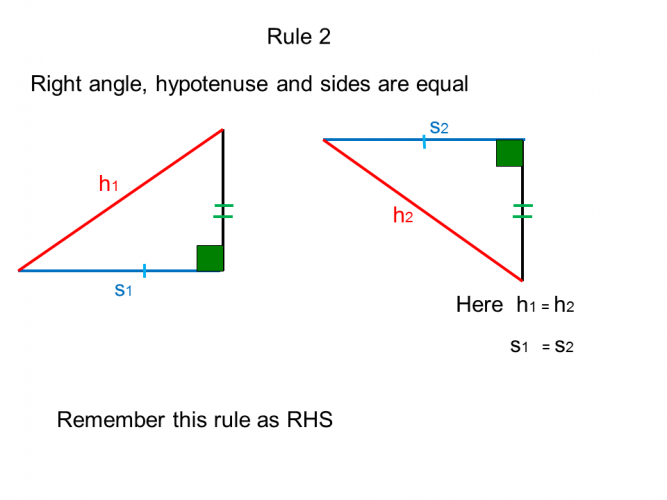
In maths, we come across congruent triangles mainly, but occasionally other congruent shapes.

 

A congruent shape is one which is exactly the same shape and size as another, but it may have been rotated.

 

 When this occurs, it can be useful to know and apply the rules the rules of congruency so that we can solve a related geometric problem. 

 

 

Let's look at these rules now...

 

 

 

 

As we can see in these diagrams, all the shapes are the same size.

 

However, we need to be able to identify the corresponding sides and angles, which can be a little tricky when the shape in question has been rotated. 

 

 

Let's have a go at identifying congruent shapes in some activities now. 

 

In this activity, we will put the four rules above into practice by identifying when they do and do not apply, plus solve problems where their application allows us to reach the correct answer.