Find Internal and External Angles in Polygons

What is your favourite computer game? How long do you spend playing it?

Do you know that calculating angles is extremely important within computer games? Interior and exterior angles are used in compiling 3D graphics.

Let's remind ourselves how we can calculate these types of angles. 

 

 

How to calculate the sum of a polygon's interior angles
 

The interior angles of a shape are all the angles on the inside.

To calculate the sum of the interior angles, we use the following formula:
 

(n - 2) x 180

where n = the number of sides 

 

If the shape is "regular", it means all the angles within the shape are equal. To then work out one individual interior angle, we then divide this answer by the number of sides:

 

Example
 

 

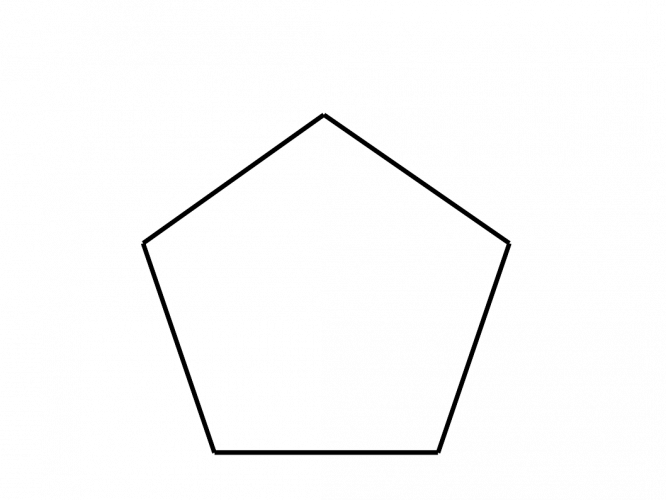
e.g Find the value of interior angles of the pentagon shown above. 

 

Sum of interior angles =

(n - 2) x 180

(5 - 2) x 180

3 × 180 = 540°

So, we know that the angles inside a pentagon add to 540°.

 

To work out one individual interior angle, we divide by the number of sides:

540 ÷ 5 = 108° 
So, each angle in a regular pentagon is 108°. 

 

 

How to calculate exterior angles

 

Exterior angles are on the outside of the shape. Let's investigate the relationship between the interior and exterior angles now.

 

e.g. Find the value of the exterior angle of the pentagon shown below. 

 

 

 

If we place an interior angle next to its exterior counterpart, they will create a straight line. 

We know that there are 180° in total in a straight line. 

So if we know one of the interior angles, we just subtract from 180 to find the exterior: 

180° - 108° = 72°

 

Example

 

Let's put all of these rules into practice now using a new example. 

 

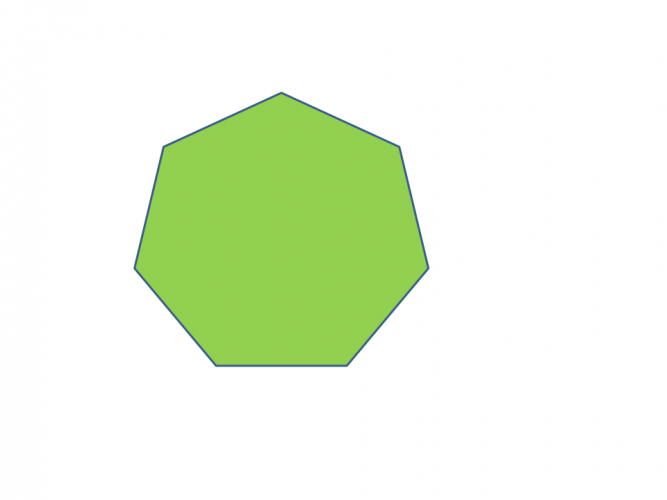
e.g. Find the interior and exterior angle of this heptagon.
 

To find the value of the interior angles:

sum of interior angles = (n - 2) x 180

= 5 × 180 = 900°

each interior angle = 900 ÷ 7 = 128.5°

 

To find the value of the exterior angles:

360 ÷ 5 = 51.5°

 

Let's check that these two angles add together to make 180° (value in a straight line): 

128.5° + 51.5° = 180°

 

 

 

Fabulous - it's time to get off the computer games and get to work now!

 

In this activity, we will use the rules illustrated above to calculate the interior and exterior angles of regular polygons with a variety of different sides. We will also use these formulae to find the number of sides of a shape or solve related problems.