Solve Problems Involving Parallel Lines

Parallel lines have so much in common - it's a shame they will never meet!

Engineers, architects and designers all need to know and use key facts about angles and straight lines in their work - we wouldn't want a wonky house or an aircraft with uneven wings, would we? 

 

Knowing the properties (facts) of angles and parallel lines can help us to solve all sorts of problems.

Let's remind ourselves of four key facts now...

1. Angles on a straight line add up to 180º

 

 

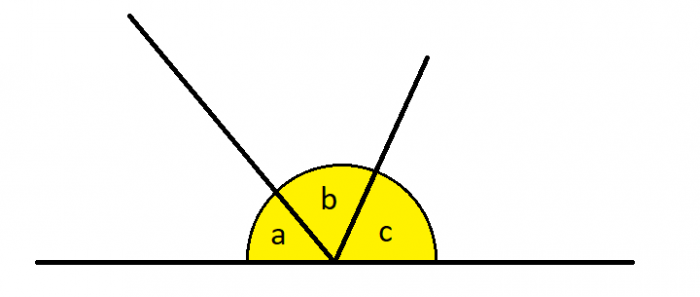
In this example, a + b + c = 180º

 

2. Interior angles add up to 180º

 

 

If we draw a letter "C" with the lines, we effectively create the interior of a shape. Here, the two purple angles add to 180º

 

3. Alternate angles (or "Z-angles") are equal:

 

If we use the parallel lines to draw a letter "Z", the two angles in its corners are equal. This works inside and outside the "Z". In other words, the two red angles are equal, and the two orange angles are equal. 

 

4. Corresponding angles (or "F-angles") are also equal:

 

Finally, if we use the parallel lines to draw a letter "F", the two angles it creates inside the "F" are equal. It also creates a pair of matching angles that sit on top of each "arm" of the letter F. In the examples above, the two green angles are equal, and the two blue angles are equal.

 

Often we will see more than one of these rules in action within the same problem, so we need to have our eagle eyes ready to spot these scenarios.

 

Let's give this a go now in some examples. 

 

e.g. Find the value of angle x in the diagram below:

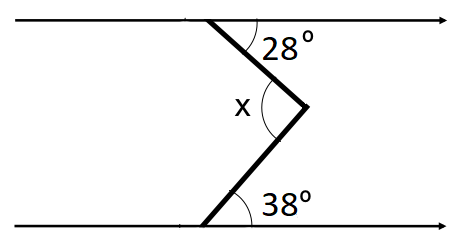
Here, we need to draw another parallel line through the centre of our diagram to help. 

Don't worry, there are no rules to say that we can't do this!

 

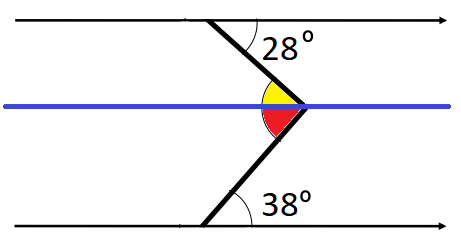
This has split our target angle (x) into two smaller angles.

We can now apply the alternate angle rule from above to see that the yellow angle is 28° and the red angle is 38° 

Therefore, x = 28° + 38° = 66°

e.g. Find the value of x and y in the diagram below:

 

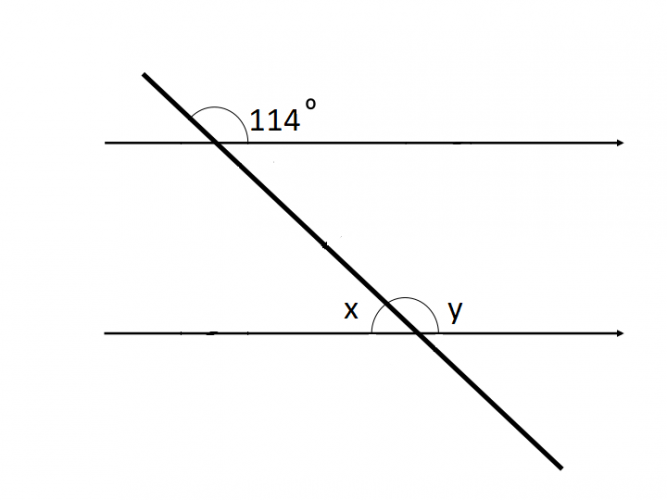
Angle y is a corresponding angle to 114° so these must have the same value. 

Therefore, y = 114°

Angle x and y are on a straight line, so together will add up to 180°. 

Therefore, x = 180° - 114° = 66°

Now we are going to put all the rules we know relating to angles and straight lines together to solve problems which involve taking multiple steps to calculate unknown angles using number and algebra.