
If you are the mouse on the see saw above, it makes sense that you wouldn't want to face the elephant opposite you.
You would want someone opposite you of the same size, to make things equal and moving the seesaw a lot easier!
There are lots of things in maths that are equal; a fact which often makes problems easier for us to solve as a result.
When two lines intersect with each other (cross over), four angles are formed.
The pair of angles which lie opposite each other at the point of intersection are called vertically opposite angles.
Vertically opposite angles are equal as shown in this diagram:
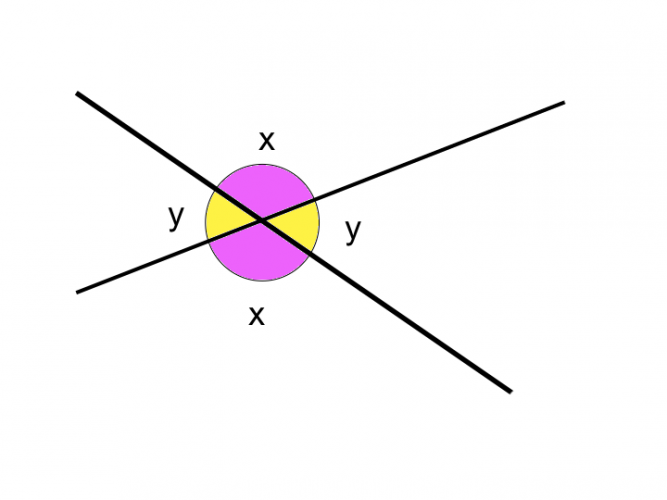
The two angles labelled x are equal, and the two angles labelled y are equal.
As an added extra, the angles on each of the straight lines add up 180°.
x + y = 180°
If we think about this, it makes sense because all the angles around a point make a circle and add up to 360°.
Right then, let's put what we know into action now.
In this activity, we will use the key fact, that vertically opposite angles are equal, to find the value of unknown angles using number and algebra and solve problems involving vertically opposite angles.








