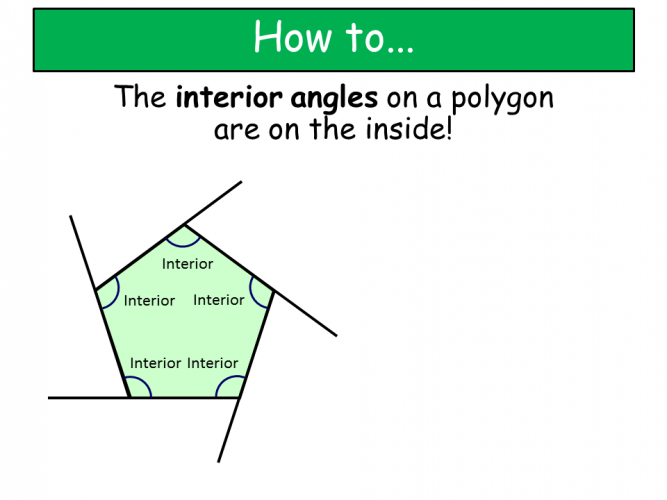
Polygon is the name given to any 2D shape with straight sides.
A regular polygon has all sides and angles which are the same, whilst an irregular polygon has different side lengths and angles.
Read on to explore some key facts relating to polygons and their interior angles.
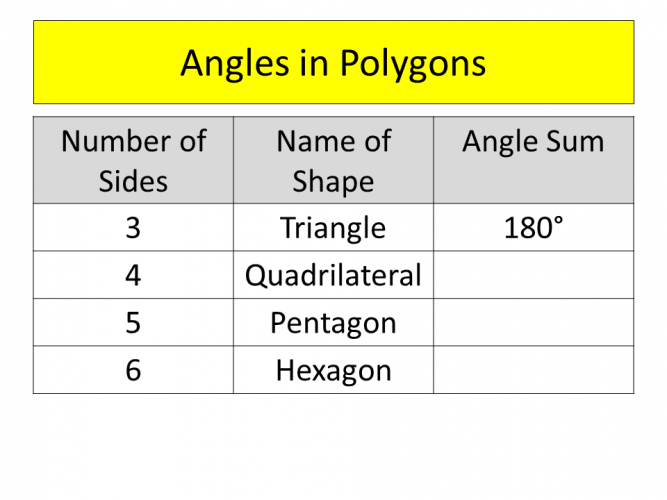
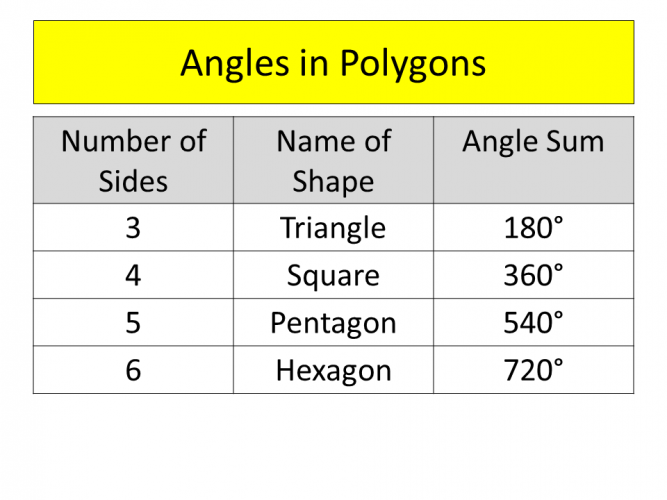
This table summarises the information you hopefully already know about polygons and their interior angles:
We know that a triangle has angles that add up to 180°.
Did you know that we can use this fact to help us find the sum of the angles in any polygon?
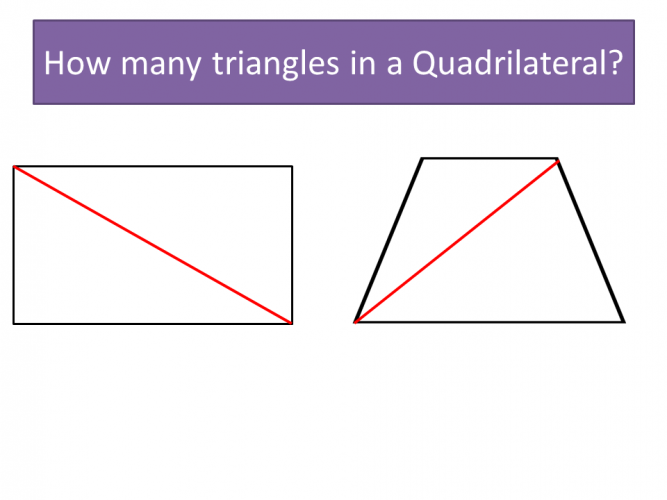
As you can see in the diagram above, we can split a quadrilateral into two triangles.
Each triangle has three angles that add up to 180°, therefore 180° + 180° = 360°.
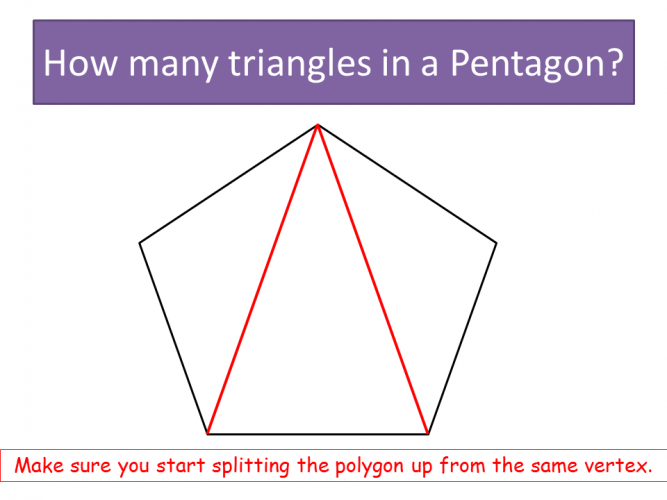
Here, we can split a pentagon into three triangles.
Therefore, 3 × 180° = 540°
Can you spot the pattern?
4 sides = 2 triangles × 180°
5 sides = 3 triangles × 180°
Can you see that the number of triangles in a polygon is always two less than its number of sides?
We can make a formula from this:
Sum of the degrees in a polygon = (number of sides - 2) × 180
Therefore, for a hexagon (6-sided shape), we don't need to draw the shape to find the angle sum, we can just work it out:
6 - 2 = 4
4 × 180° = 720°
So our final summary table will look like this:
If we know the sum of the angles in a regular polygon, how do we find the size of a single angle?

All we need to do is take the sum of all the angles, then divide this by the number of sides present.
e.g. The interior angle of a pentagon is:
540° ÷ 5 = 108°
And finally, if we are given an interior angle, we can find the number of sides of the shape, like this:
Interior angle = 150°
180 - 150 = 30
360 ÷ 30 = 12 sides
Now let's put all these facts and formulae into practice in some real questions now.
In this activity, we will calculate angle sizes within polygons. We will also find the number of sides of a polygon when given an interior angle.