Do you need an arc?
I Noah guy.....
Apart from the ark that Noah built, there is another kind.
As you can see from the diagram below, an arc is a part of the circumference of a circle.
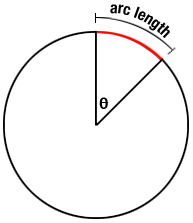
Probably the only time you will need to calculate the length of an arc is in maths lessons. (Unless Noah offers you a job)
Maths is a little bit like building Noah's ark.
It is easy if you read the instructions carefully.
Instructions in maths come in the form of a formula.
Being part of a circle, pi  is involved of course.
is involved of course.
Circumference of a circle is π x diameter (πd)
Since an arc is part of the circumference, it makes sense to use this as part of our calculation:
Length of an arc = angle ÷ 360 x π x diameter
Generally in maths questions, you're given the radius of the circle - you could double the radius to get the diameter or the formula applied could be:
Length of an arc = angle ÷ 360 x 2 x π x radius
Remember you can use the π button on your calculator or use the values 3.14 or 3.142 in your calculations.








