You should be familiar with the word "quadrilateral" meaning a four-sided shape.
In this activity, you will examine cyclic quadrilaterals and work out missing angles.
What is a cyclic quadrilateral?
A cyclic quadrilateral is a four-sided shape enclosed within a circle, as shown below:
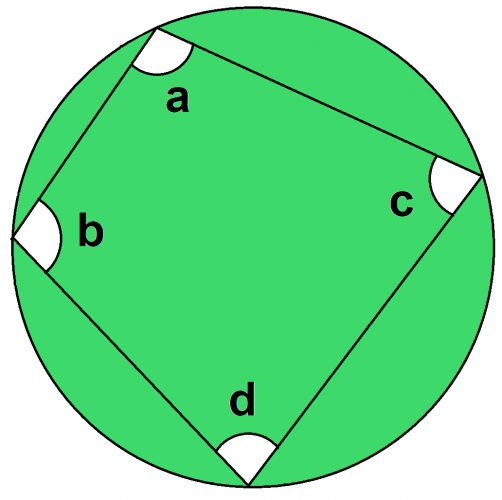
The rule that you need to remember is that opposite angles in a cyclic quadrilateral add to 180°.
So in the diagram above, a + d = 180° and b + c = 180°.
By extension, this means that the total angles in a quadrilateral will add up to 360°.
But, be careful!
The rule only works if all four corners of the quadrilateral touch the circumference.
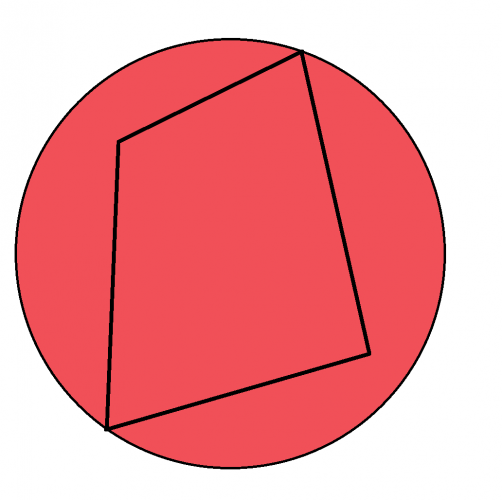
The quadrilateral inside this circle is not a cyclic quadrilateral because only two of its corners are touching the circumference. Its total angles add to 360°, but its opposite angles do not add to 180°.
In this activity, we will find the value of unknown angles and solve problems requiring the application of the theory explained above.
As ever in circle and angle investigations, we will be asked to recall other angle properties too.







