Did you know that mathematicians have been studying circles for centuries, pretty much since the invention of the wheel?
Who would have thought that the humble wheel could keep us working all these years later.
Every maths teacher you have ever had, will have taught you something about circles, which combines together to form your toolkit of circle knowledge.
Are you able to follow what your maths teacher says all of the time?
Or do they go off on a tangent?
Do you go off on a tangent?
Going off at a tangent can help us with circle theorems.
It can help us identify some key properties (facts) about the circle we are investigating.
Lets investigate this further by identifying some key uses of tangents in circle theorem...
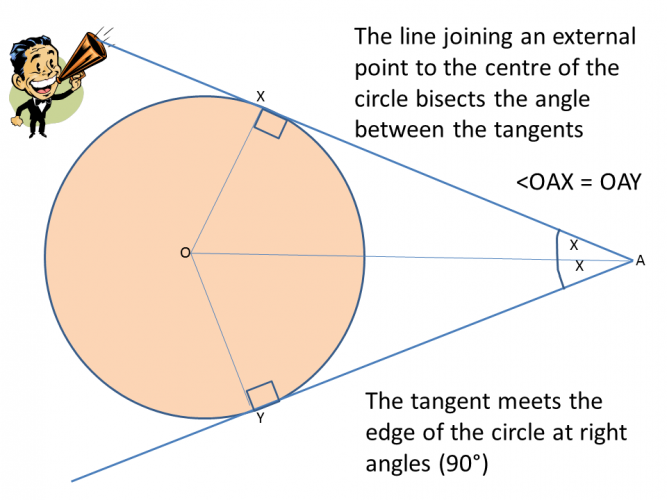
Also, the radii from the centre of the circle are of equal length, which means that a quadrilateral has been formed.
These facts and uses of tangents can help us to solve circle problems - let's check out some examples to see this in action.
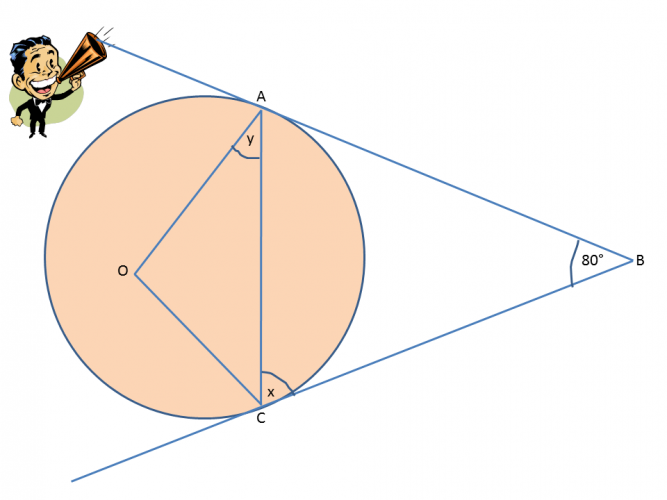
e.g. Find the value of angle x in the diagram below:
Can you see where the tangents meet the edge of the circle?
This forms an isosceles triangle (which is a triangle with two side lengths that are the same and two base angles that are the same).
We can now work out angle x using the fact that there are always 180° in a triangle:
180 - 80 = 100°
x = 100 ÷ 2 = 50°
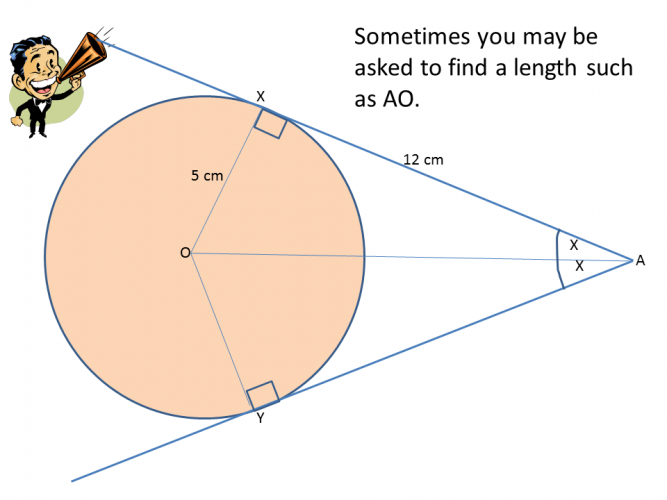
e.g. Find the distance between point A and the centre of the circle (O):
As right angles have been formed between the tangents and the radii of the circle, we can use Pythagoras' Theorem to find AO:
12 cm² + 5 cm² = 169 cm²
√169 = 13 cm
Ready to chase these problems down now?

In this activity, we will find the value of unknown angles and lengths and solve problems requiring the application of the tangent theorem explained above.
As with all circle theorems, we will need to recall other angle and shape properties as well, so watch out for these.