BACK TO WORKSHEETS
There are some questions in Higher GCSE exam papers where you need to calculate lengths of triangles using trigonometry without a calculator.
The only way to solve these types of question is to learn exact trig values.
The values of sin, cos and tan that you need to know are those for 0°, 30°, 45° 60° and 90°.
Deriving the values
Take an equilateral triangle, giving each side a unit of 2:
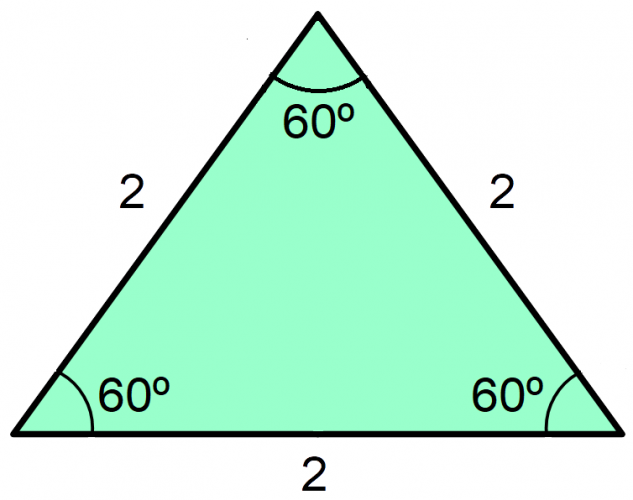
Now cut it in half to make a right-angled triangle as shown:
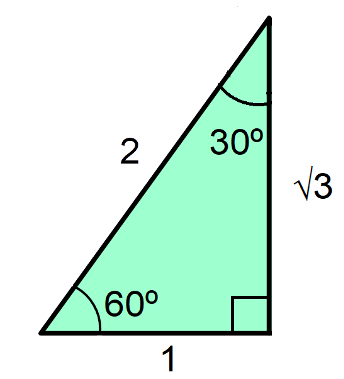
Using Pythagoras, we can deduce that the vertical side is √3.
We now have a right-angled triangle with three known lengths and angles. It means we can apply sin, cos, and tan to work out their values for 30° and 60° by considering opposite, adjacent, and hypotenuse sides and using "SOH CAH TOA":
sin 60 = √3/2
cos 60 = 1/2
tan 60 = √3/1
sin 30 = 1/2
cos 30 = √3/2
tan 30 = 1/√3
Now, consider a right-angled isosceles triangle as shown:
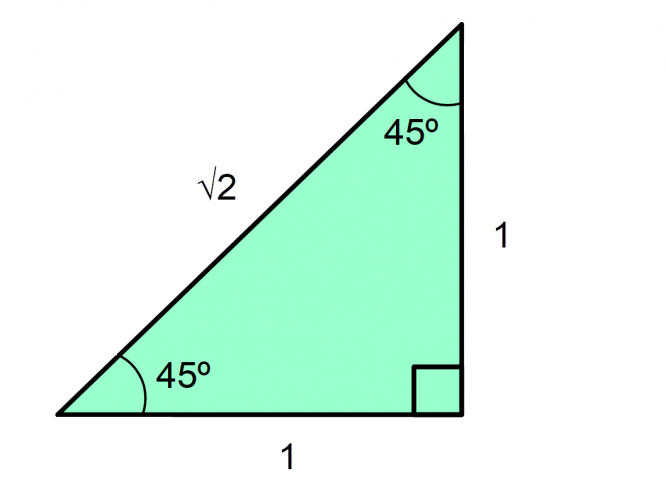
We can give the two shorter lengths a unit of 1, and using Pythagoras, deduce the hypotenuse is √2.
Once again, we can use "SOH CAH TOA", this time to work out all the values for 45°:
sin 45 = 1/√2
cos 45 = 1/√2
tan 45 = 1/1
Learning the table
The table below summarises all the values you need to learn.
Each value has been simplified and rationalised.
| sin | cos | tan | |
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | - |
As well as the values we calculated from our triangles above, you also need to be familiar with sin, cos, and tan of 0° and 90°.
Tips for remembering the table
- The columns for sin and cos are the same list of values, but in reverse order.
- cos is the only trig ratio that doesn't have a value of zero at 0°.
- tan x = sin x / cos x. This means you can derive any value for tan by dividing sin and cos of the same angle. (e.g. tan 60 = sin 60 / cos 60 = √3/2 ÷ 1/2 = √3)
- tan 90 has no value because it would require us to divide 1 by 0, which is infinity.
