Apply the Properties of Quadrilaterals

 

Have you ever ridden one of these?

 

This is called a quad bike, and it certainly looks like a lot of fun! Did you know that the prefix "quad-" means four?

 

Can you think of any other words that use this prefix? We have quadruplets, quadruple, quadratic, and, of course, a quadrilateral. 

You need to be able to recall that any four-sided shape is called a quadrilateral. 

 

 

There are several important quadrilaterals which we need to be confident to recognise and work with in maths problems. 

 

They all have different properties (facts) which relate to them, so let's review these now, before we start working on some related problems.

 

 

Let's start with the most obvious quadrilateral, which really demonstrates that "quad" means "four". Squares have four equal sides, four right angles, four lines of symmetry, and a rotational order of symmetry of four.

 

 

Next, we have a rectangle. This has all the same properties as a square, except it has two pairs of matching lengths, and only two lines of symmetry and a rotational order of two.  

 

 

A parallelogram is like a rectangle without the right angles. It has two opposite pairs of parallel sides but no lines of symmetry. The order of rotational symmetry is two. Another property of the shape is that the opposite angles are equal.

 

 

 

A rhombus looks very similar to a parallelogram. The difference between the two shapes is that, in a rhombus, all four lengths are equal. (You may sometimes see this shape called a "diamond"). Like a parallelogram, it also has rotational symmetry order two, but it has two lines of symmetry rather than zero. Its opposite angles are also equal.

 

 

A kite consists of two adjacent pairs of equal length and one pair of equal angles. It has one line of symmetry and a rotational symmetry order of one.  

 

 

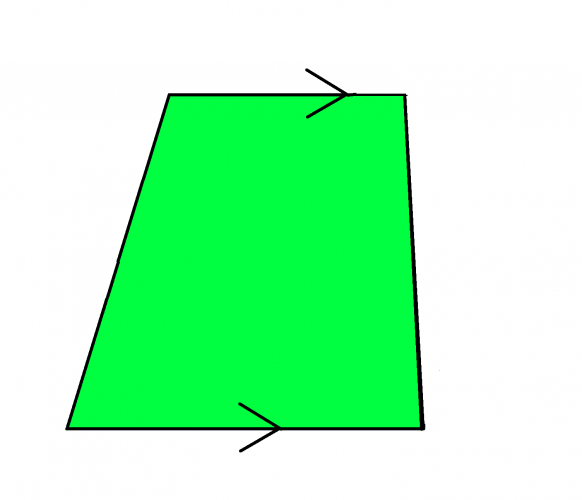
Finally, we have a trapezium. It has one pair of parallel lines and no lines of symmetry. This particular type of trapezium is called a scalene, as all four sides are different lengths. There are two other varieties of trapezium to be aware of:

 

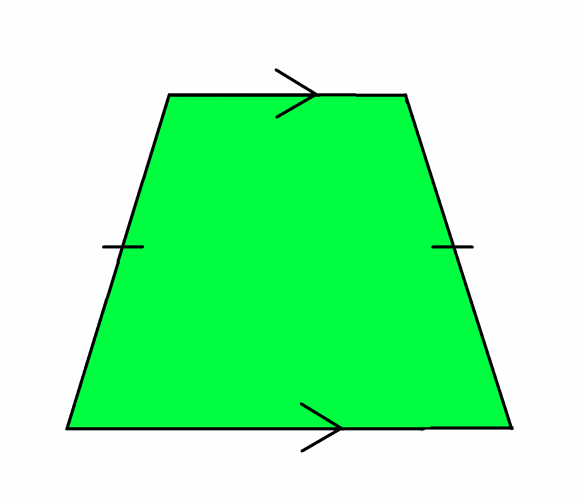
An isosceles trapezium has two equal lengths (think of an isosceles triangle with the top cut off). It is the only type of trapezium that has a line of symmetry.

 

 

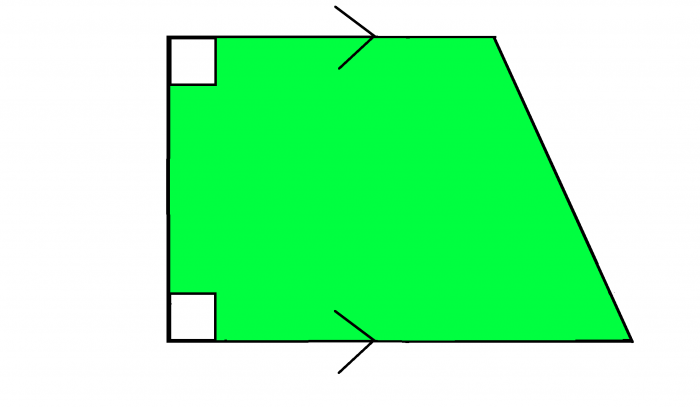
The last shape on this list is a right trapezium. It has the same properties as a scalene trapezium, except it also includes a pair of 90° angles.

 

 

And finally, one absolutely key fact that applies to all the above shapes: the sum of the angles inside a quadrilateral is always 360°.

 

 

Now let's put these properties into practice in some geometric problems now. 

 

In this activity, we will practise recognising quadrilaterals and solving geometric problems which require understanding and application of their key properties.