Apply the Angles in the Same Segment Rule

Circles are all around us in everyday life.

 

How many examples can you think of?

 

Can you see any circular shapes in objects around you at this moment?

 

 

Mathematicians have investigated circles for centuries because of their love of pure mathematics.

The ability to learn, understand and apply circle theorem is an essential, but challenging, geometric skill. 

For this reason, we usually only see circle theorem questions on the Higher GCSE exam paper. 

It is also common for circles and angles to be linked in questions, so we may need to apply our knowledge of angle properties too. 

 

 

In this activity, we will focus on one specific theory relating to circles:

 

 

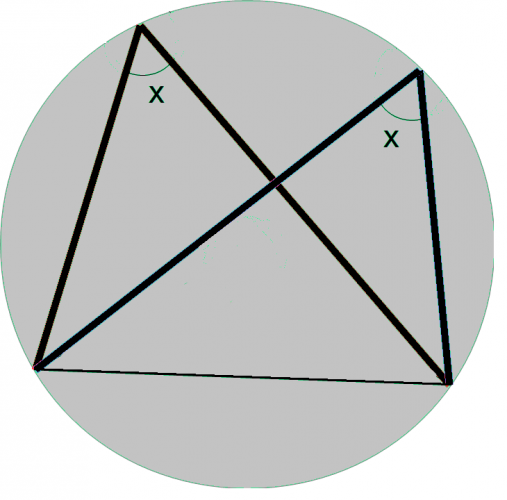
Angles in the same segment are always equal. 

 

 

Let's now look at how this theory works and why it is always true. 

 

 

 

Let's begin with a circle and mark its centre.

 

 

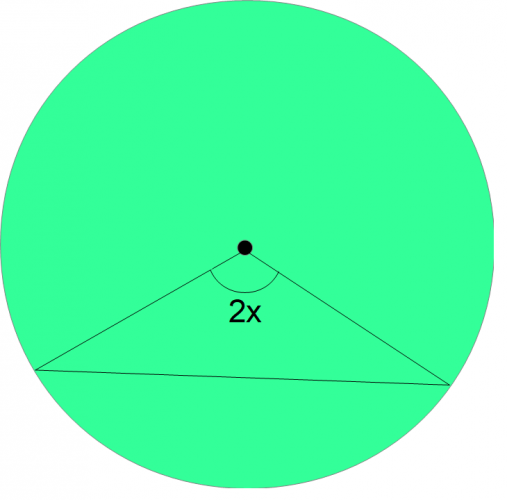
We can draw two radii coming from the centre, and join them with a chord to create an isosceles triangle. Let's call the angle at the centre of the circle 2x.

 

 

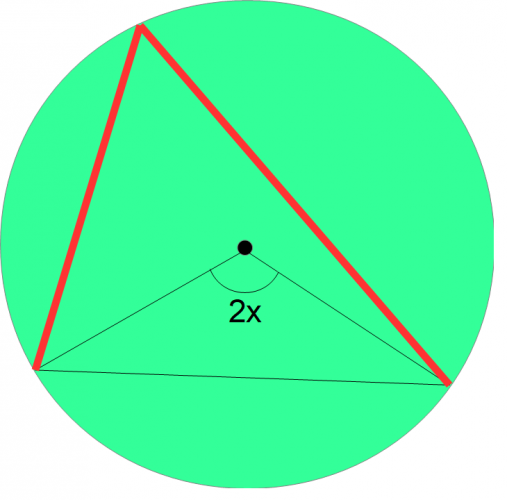
We can now use the chord as the base for a new triangle (shown in red) that touches the circumference.

 

 

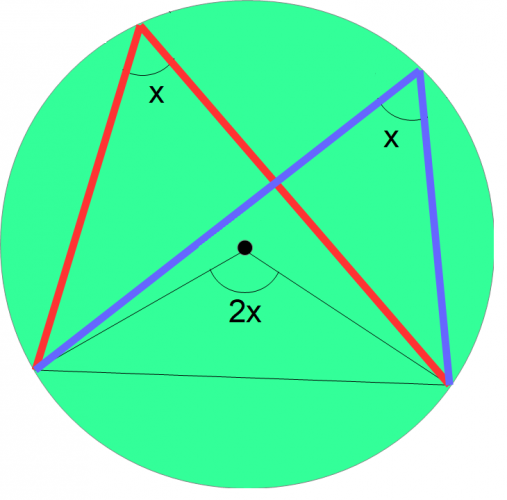
Finally, let us draw another triangle from the same base that touches the circumference (shown in blue).

Angles at the circumference are alwas half the size of angles at the centre of a circle. As the angle at our centre is 2x, the two angles at the circumference created by the triangles are x. In other words, they are equal. 

 

Let's put this theory into practice now in some geometric problems.