Circles are all around us in everyday life.
How many examples can you think of?
Can you see any circular shapes in objects around you at this moment?
Mathematicians have investigated circles for centuries because of their love of pure mathematics.
The ability to learn, understand and apply circle theorem is an essential, but challenging, geometric skill.
For this reason, we usually only see circle theorem questions on the Higher GCSE exam paper.
It is also common for circles and angles to be linked in questions, so we may need to apply our knowledge of angle properties too.
In this activity, we will focus on one specific theory relating to circles:
The angle of two points meeting at the centre of a circle is twice the angle of the same points meeting at the circumference.
Let's see this theory in action on a diagram:
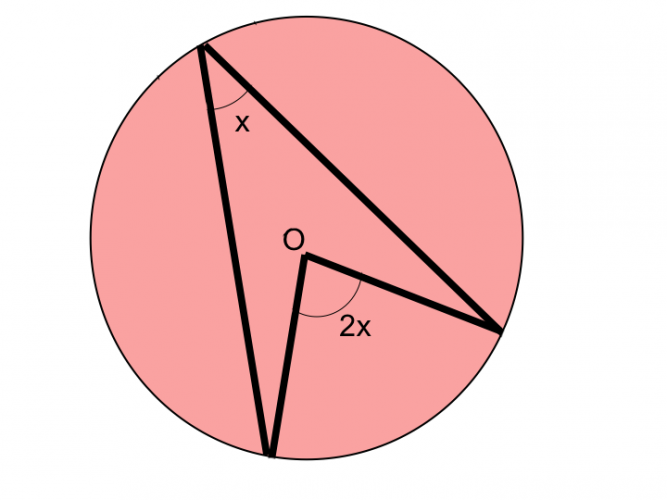
Example
If the angle at the circumference is 38° the angle at the centre will be 76°:
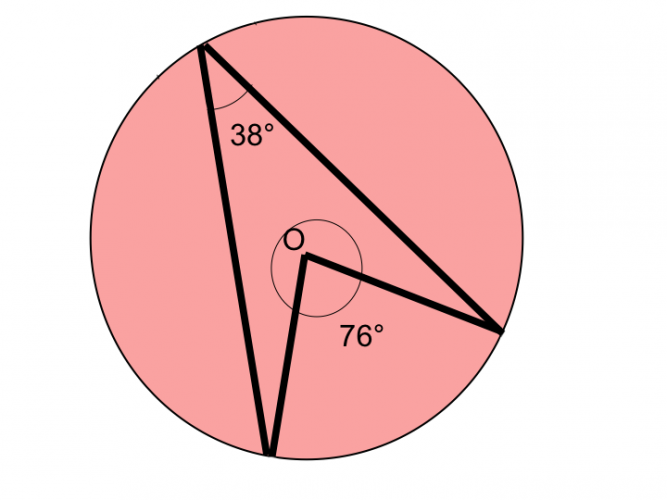
So applying this theory means that we can simply halve the central angle to find the circumference angle, or double the circumference angle to find the central angle.
The only circumstance which must be present for this rule to apply, is that both angles must be created from the same two starting points.
Let's put this theory into practice now in some geometric problems.







