What is a chord?
A chord is the line segment joining two points on a curve.
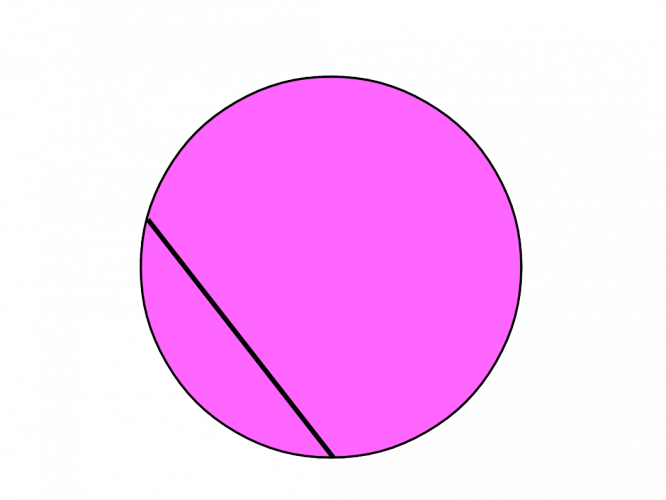
You can think of it this way: a chord is a straight line that touches the circumference twice. A chord is different to a diameter because it doesn't pass through the centre of the circle.
Chords in circle theorems
If a radius of a circle bisects a chord, they will create a right angle and the lengths to either side will be equal:
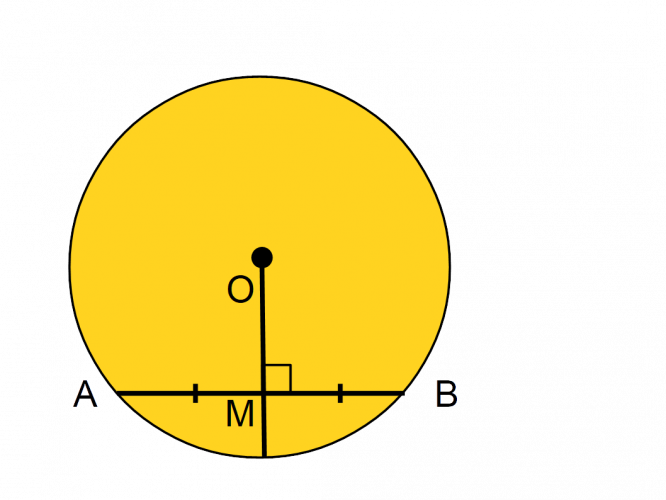
In this circle, A and B are points on the circumference. O is the centre and M is the point where the radius and chord intersect.
Length AM = BM.
Angle AMO = BMO = 90º.
These facts can be combined with other theorem to find missing angles or sides within a circle - let's explore how in some examples.
Example 1
e.g. What is the value of angle x?
.png)
The rule to use here is: where the radius bisects the chord, a right angle will be created.
We also know that there is always 180° in total within a triangle.
So to find angle x, we can subtract the two known angles from 180° to find x:
180 - 90 - 48 = 42°
Example 2
Calculate length x.
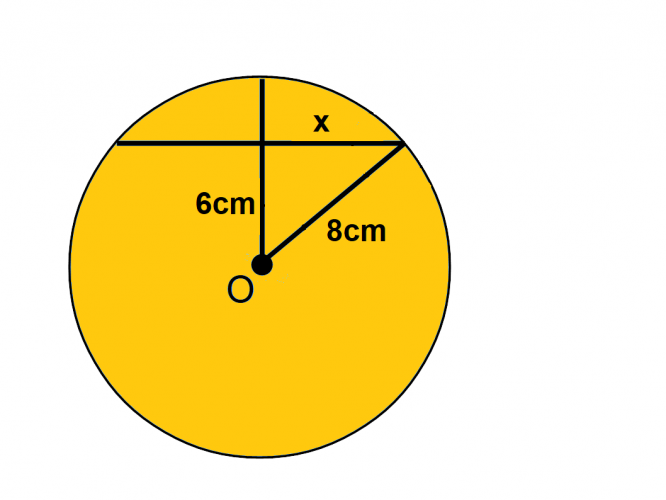
As the chord cuts the radius at a 90° angle, we know that a right-angled triangle has been formed.
So, we can apply Pythagoras' Theorem to find our missing side length (x):
a² + b² = c²
6² + x² = 8²
8² - 6² = x²
√ 28 = 5.29 cm
In this activity, we will use the facts detailed above to find missing angles or side lengths.
As with all circle theorems, we will need to recall other angle and shape properties as well, so watch out for these.







