Here's another theory to add to your circles toolkit.
This time, we will focus on the theory that:
Angles in alternate segments within a circle are equal.
Let's use a diagram to illustrate this scenario in action...
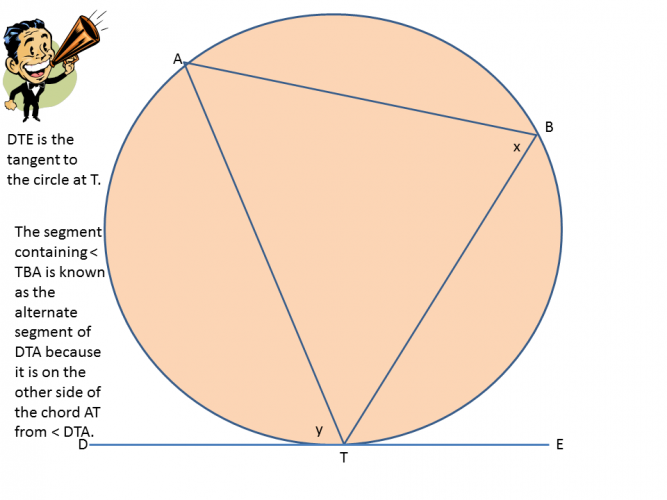
We can see that the circle above has been divided into segments from the starting point T.
The line DTE is a tangent to the circle.
(Remember a tangent is a line that touches the circle at exactly one point, never entering the circle's interior.)
Look at the angles x and y on the diagram:
The rule here is that the angle between a tangent and a chord is equal to the angle in the alternate segment, so angle x and y in this diagram have the same value.
Let's use an example with real numbers now.
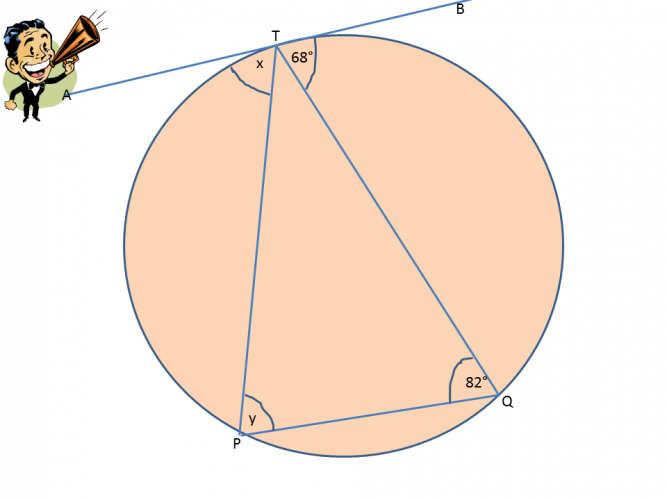
e.g. What are the values of angles x and y shown in the diagram below?
Angle x is in the alternate segment to 82°, so therefore has the same value.
Angle y is in the alternate segment to 68°, so has the same value too.
In this activity, we will find the value of unknown angles and solve problems requiring the application of the theory explained above.
As with all circle theorems, we will need to recall other basic angle properties as well, so watch out for these.