Apply Circle Theorems to Solve Problems

What did the caveman say to his mate?
Do you want to go clubbing tonight?
We have a lot to thank the caveman for - or whoever it was that invented the wheel!
Circles are a huge part of our everyday life, from a potter's wheel, jewellery and clocks, to perhaps the most important use of all - wheels.
Engineers owe a lot to the study of circles, as gears rely on them. Can you think of any more uses?
Circle theorems help to solve problems in many ways.
Let's remind ourselves of the theorems:
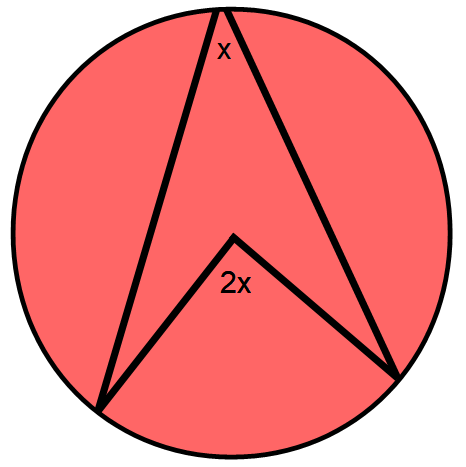
Angles at the centre are twice that on the circumference:
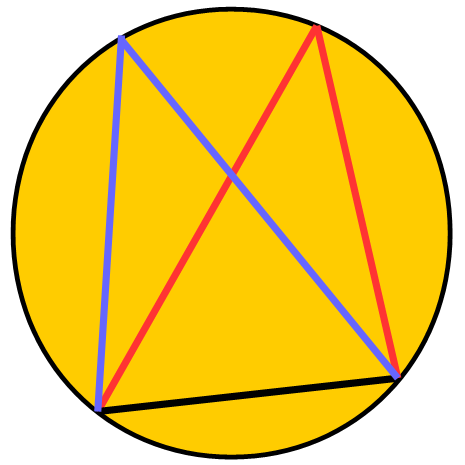
Angles in the same segment are equal:
In other words, two triangles enclosed in the same segment are identical. In this example, the red and blue triangle are identical because they are both drawn from the same chord and both touch the circumference.
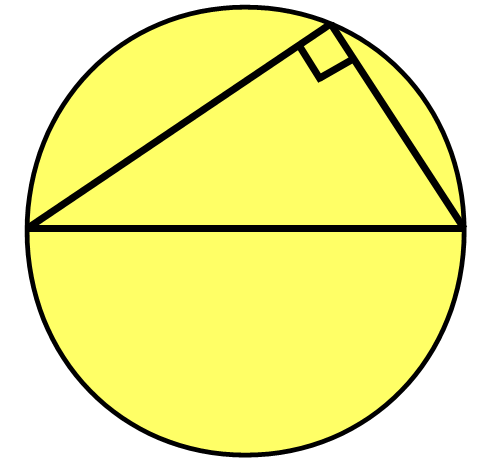
Angle subtended from the diameter is 90°:
Opposite angles in cyclic quadrilaterals add up to 180°:
Here, a + c = 180° and b + d = 180°
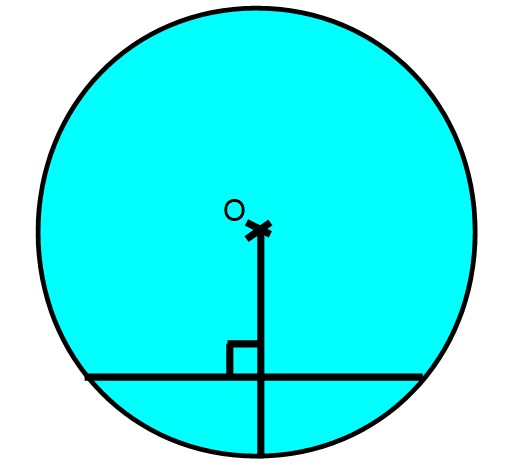
Chords meet radii meet at 90 degrees:
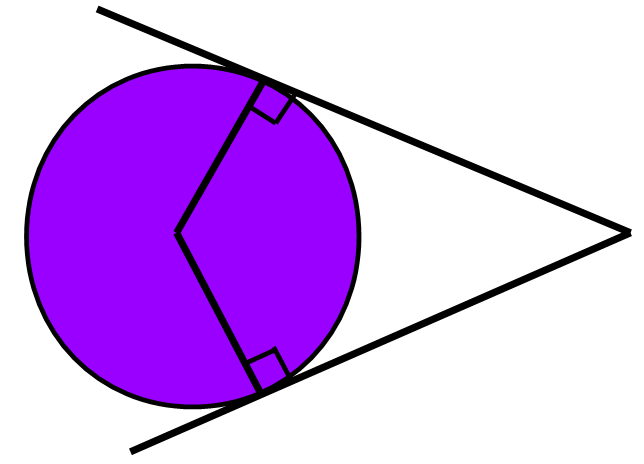
Tangents to a circle meet the circumference at 90° and the lines are of equal length when they come from the same point:
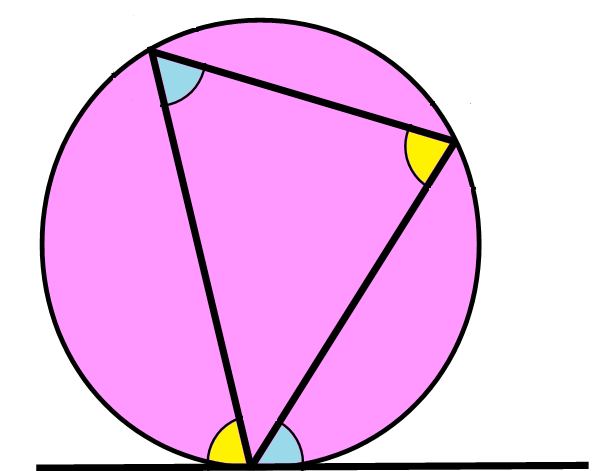
Angles in alternate segments are equal:
This is perhaps the most complicated theorem, but think of it this way: when a triangle is enclosed inside a circle and a tangent meets the circumference as in the example above, the two angles shaded in yellow are equal and the two in blue are equal.
The trick to being successful in these questions is to be able to spot the theorems.

In problem-solving questions, there is usually more than one theorem to follow.
Quite often you will have to find angles that are not identified first.
Let's investigate the magic...