Find the Hypotenuse Using Pythagoras' Theorem

 

Guess who?

I was born 2500 years ago on the island of Samos.

At the age of 18, I went to work for an astronomer.

At the age of 21, I went to Egypt to learn about geometry.

On my return to Greece, I opened a school in mathematics, music, philosophy and astronomy.

 

Answer

 

 

Pythagoras is best known for the following formula that allows us to find missing sides of right-angled triangles:

a² + b² = c²

Here, we will look at what it means and how to use it.

First, let us understand what the letters stand for:

 

 

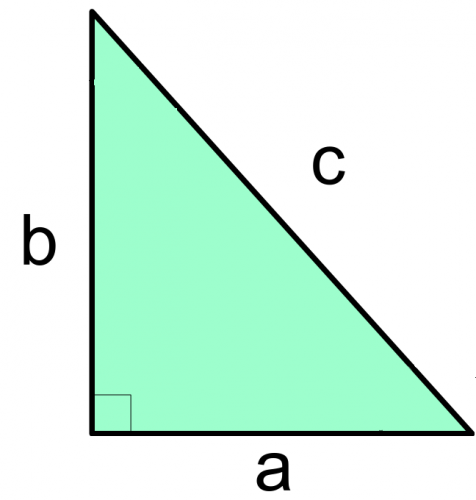
On any right-angled triangle, the longest length is called the hypotenuse. This is the "c" in the formula. 

The other two lengths are called "a" and "b". It does not matter which way round these are labelled.

In this activity, we will learn how to find the hypotenuse of triangles.

 

Example

Find the length of c

 

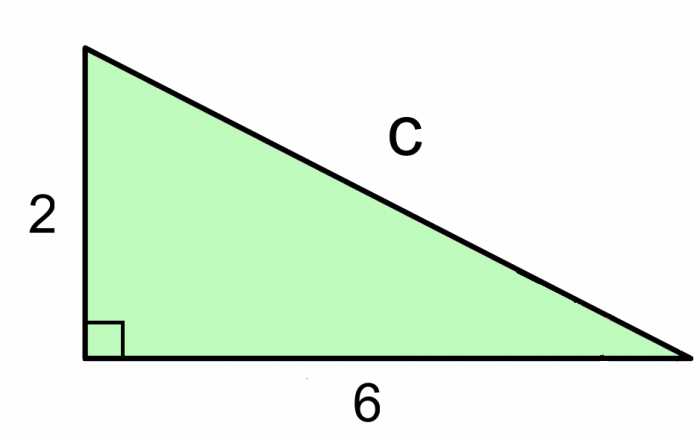
Using the formula a² + b² = c² this can be solved in three steps:

 

1.  Square both sides.
2 x 2 = 4
6 x 6 = 36

2. Add your answers together
4 + 36 = 40

3. Square root
√40 = 6.32 (to 2 decimal places).

 

And there you have it! You can find the hypotenuse of a right-angled triangle!

It is important to note that the hypotenuse isn't necessarily labelled as "c" - it can be called any letter and the formula will still work. 

Now that you have seen the formula and how to use it, have a go at some questions to test your understanding!