You should be confident at recalling Pythagoras' theorem:
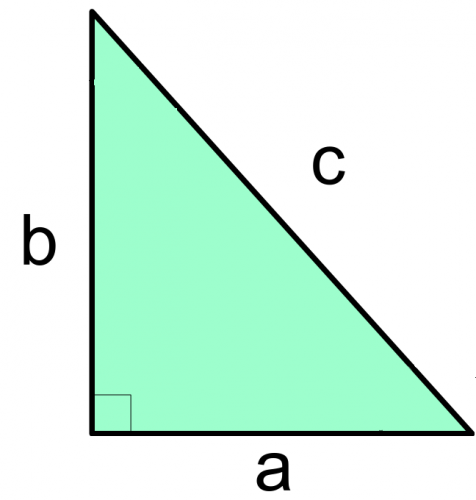
a² + b² = c²
a and b are the shorter sides of a right angled triangle and c is the hypotenuse.
Sometimes you will need to find a shorter side, so this will require you to rearrange the formula.
Rearranging for a gives:
a = √(c² - b²)
Substituting lengths c and b into the formula will instantly find the shorter side.
Let's take a look at an example:
Find length a of this triangle.
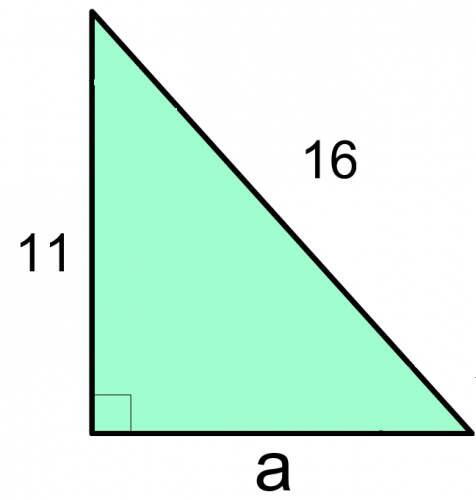
The formula gives:
a = √(c² - b²) = 11.62 (to 2 decimal places).
1. Square both sides.
16 x 16 = 256
11 x 11 = 121
2. Subtract your answers
256 - 121 = 135
3. Square root
√135 = 11.62 (to 2 decimal places).
Think of it this way: "square, square, subtract, square root".
Remember: if it is the shorter side you want to find, your answer will never be larger than the length of the hypotenuse.
This is a good way to evaluate whether your answer is correct. It is always important to check.
Now that you have seen the formula and the method, write it down and test your understanding with this activity.








