While there are four transformations we have to learn for GCSE success, there are only three transformations that will allow an object to keep the same sides and angles (the mathematical name for this is congruency).
They are: rotation, reflection and translation.
Frequently, you will be given a shape and asked to transform it, but you could also be asked to do this the other way round and describe the transformation which has already occurred.
What information do we need to give to describe a transformation?
Each transformation has a different list of information that we must provide.
The most common cause for losing exam marks on these questions is missing one or more of the pieces of information.
The information required varies depending on the type of transformation:
Reflection: We need to give the equation of the mirror line;
Translation: We need to give the vector of the movement;
Rotation: We need to give the distance, direction and centre of rotation.
Plus, don't forget...
It's amazing that the essential fact, often missed when students complete these questions, is forgetting to define which type of transformation has occurred!
The first thing we should always state is if the transformation is either a reflection, rotation or translation.
Let's look at each type of transformation in action in an example now...
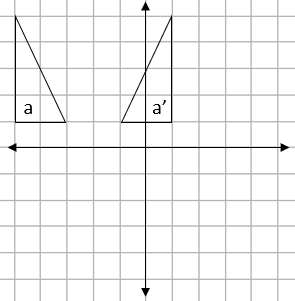
e.g. Describe the transformation shown below fully:
Step 1: Decide which transformation it is:
We can describe the movement between shape a to a' as a flip.
This means that this transformation is a reflection.
Step 2: State the information we need to give:
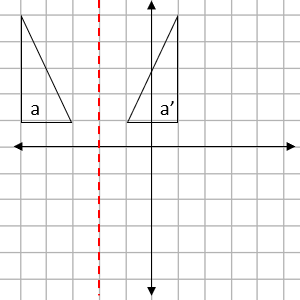
For a reflection, we need to provide the mirror line.
This will always be positioned exactly half-way between the two shapes, like this:
This mirror line passes through the x axis at -2.
This means the mirror line is defined as: x = -2.
Step 3: Put the two elements together:
We would describe this as a translation in the line x = -2.
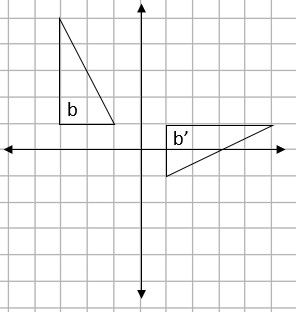
e.g. Describe the transformation shown below fully:
Step 1: Decide which transformation it is:
We can describe the movement from b into b’ as a turn.
This tells us that the transformation applied is a rotation.
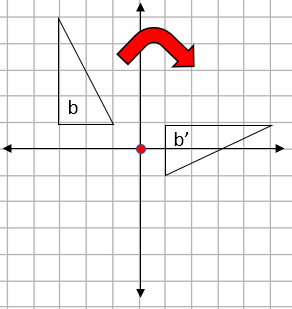
Step 2: State the information we need to give:
The easiest way to find the centre of rotation is to trace the original shape using tracing paper (you can always ask for this in an exam) and just try using some points between them as the turning point.
When you find the one that works, that is the centre:
This transformation is described as a:
Rotation of 90° (distance) in a clockwise direction around the centre (0,0).
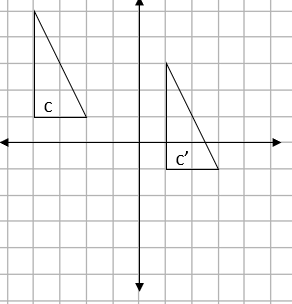
e.g. Describe the transformation shown below fully:
Step 1: Decide which transformation it is:
We can see that shape c has been slid but remained in the same orientation.
This means that the transformation applied it is a translation.
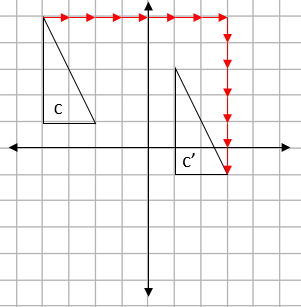
Step 2: State the information we need to give:
To describe a translation, we must provide a vector.
We can see from the arrows that are drawn below that shape c has been moved 7 squares to the right and 6 down:
We write this as the vector:
| 7 |
| -6 |
In this activity, we will identify the type of transformation which has occurred, providing the required information to describe the change accurately.
You may like to have some resources handy to help you - a pencil, squared paper and tracing paper could be beneficial. If you do not have these resources available, then you will need to be able to imagine the changes occurring in your mind's eye instead.