In geometry, two shapes or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
There are three possible transformations that will allow a shape to maintain the same sides and angles: rotation, reflection and translation.
Sometimes, we will be given a transformed object and be asked to describe the transformation.
How do we 'describe a transformation'?
Each type of transformation has a different list of information which we must provide in order to accurately describe each:
Reflection: We need to give the equation of the mirror line;
Translation: We need to give the vector of the movement;
Rotation: We need to give the distance, direction and centre of rotation.
How should we start our descriptions?
The factor that is often missed in these descriptions is the most important - we need to state which type of transformation we are seeing!
So every one of our descriptions should always start by stating if the transformation is a reflection, rotation or translation.
Congruent Vs Similar
If a shape is transformed, but doesn't change its angles or sides, it will be congruent to the original.
If a shape is transformed, doesn't change its angles but does change its sides, it will be similar to the original.
If we apply this logic to transformations, translations, reflections and rotations will produce congruent shapes, whilst enlargements will produce similar shapes.
Let's look at these principles in action now in some examples.
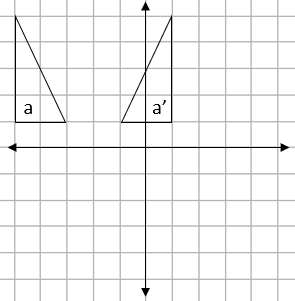
e.g. Describe the transformation shown on the grid below fully.
Step 1: Decide which type of transformation this is:
Shape a' is a flipped version of shape a, this means that the transformation we can see in action is a reflection.
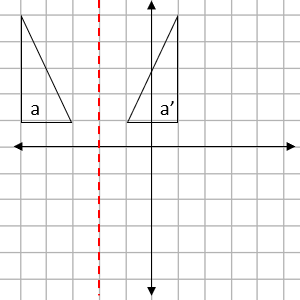
Step 2: Give the required information linked to this type of transformation:
For a reflection, we need to provide a mirror line.
This will always be positioned exactly half-way between the two shapes, like this:
This mirror line passes through the x axis at the point -2.
This means the mirror line is defined as x = -2.
Step 3: Bring this together in one sentence:
This transformation is a reflection using the mirror line x = -2.
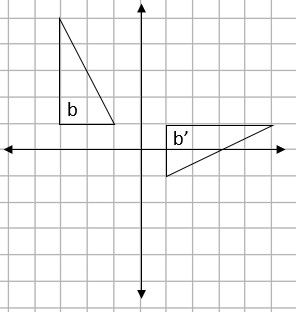
e.g. Describe the transformation shown on the grid below fully.
Firstly, we can see that this is an example of rotation.
Rotation means turning around a centre, whilst the distance from the centre to any point on the shape stays the same.
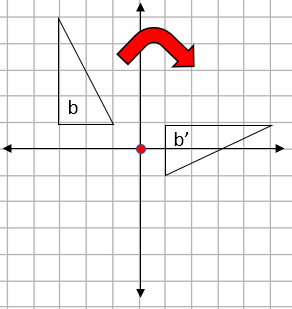
The easiest way to find the centre of rotation is to trace the original shape and try some points.
When we find the one that works, that is our centre:
This transformation is described as a rotation, with the following features:
Distance: 90°
Direction: Clockwise
Centre: (0,0)
e.g. Describe the transformation shown on the grid below fully.
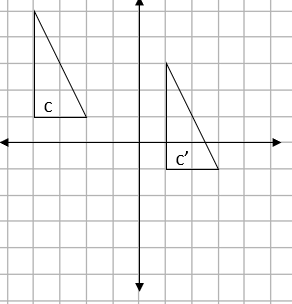
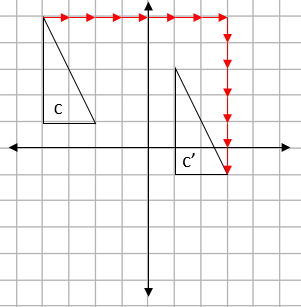
We can see that this is an example of translation.
Translation simply means moving without rotating, resizing or any other change.
To translate a shape, every point of the shape must move: the same distance and in the same direction.
To describe a translation, we need to provide a vector.
If we draw a line from one corner of the original shape to the same corner on the translated shape, we can find the magnitude of this movement:
We can see from the arrows drawn above that this is a movement of 7 squares to the right and 6 down.
We write this as the vector:
| 7 |
| -6 |
e.g. Shape A is enlarged to create shape B. Find the scale factor and centre of enlargement.
Finding the scale factor
We need to compare one of the pairs of sides.
If we use the edge of each square, shape a is 1 square long and shape b is 3 squares long.
This gives us a scale factor of 3.
Finding the centre of enlargement
To find this, we need to join up two pairs of matching corners with straight lines and see where they cross, like this:
We can see here that the two lines cross at the point (1,1) so this is our centre of enlargement.
In this activity, we will practise describing transformations by first, identifying which type of transformation we are observing, and secondly, providing the required supporting information to accurately describe each movement mathematically.
You may find it helpful to have a pencil and some squared paper handy to support you in this activity. If you do not, you will need to be able to visualise these reflections in your mind's eye.