Have you ever seen these people at the side of the road and wondered what they are doing?

They are surveyors and are calculating distances between one point and another using trigonometry.
Their apparatus can automatically work out a distance using angles and lengths, and are the type of calculations that you will practise in this activity.
Pythagoras - recap
Suppose you have a right-angled triangle, abc, as shown:
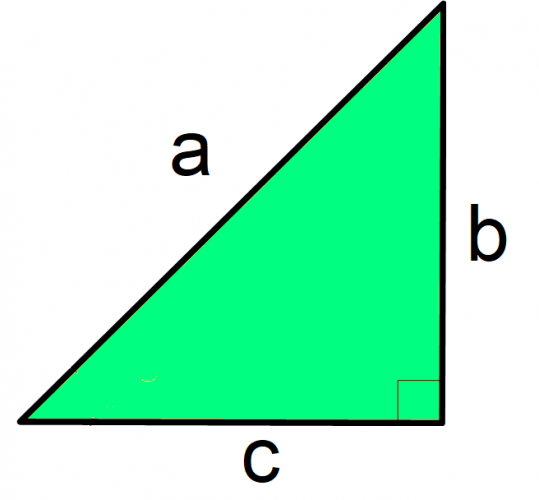
The most basic calculation for working out the length of a triangle is Pythagoras. You will be familiar with the following formula for finding the hypotenuse:
a2 = b2 + c2
You have also learned about "SOH CAH TOA" to calculate lengths of right-angled triangles, as well as the sine rule (a / sin A = b / sin B = c / sin C)
So why do we need another formula?
What is the cosine rule?
The first thing to understand about the cosine rule is that it works on any type of triangle. This makes it different to Pythagoras and trigonometry.
It is also different to the sine rule, because that requires two angles and one side to work out a length of a triangle. With the cosine rule, you need to have one angle and two sides. So knowing the difference between the sine rule and cosine rule is useful, because it will allow you to pick the correct method when solving these types of question.
Let's make a small adjustment to the triangle we saw earlier. Triangle, abc, is now shown:
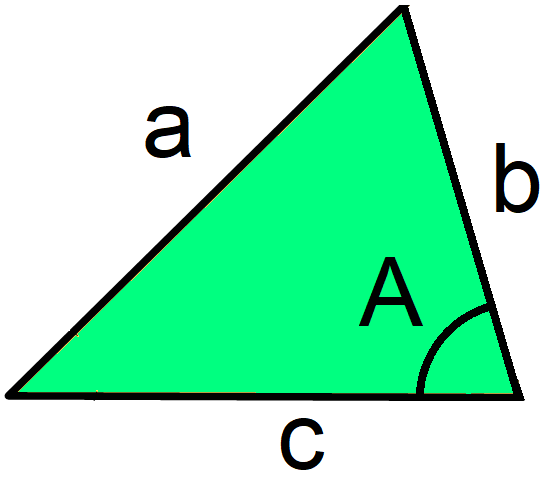
The cosine rule is:
a2 = b2 + c2 - 2bc cos A
where a, b, and c are the lengths, and A is the angle.
The first thing to notice is the similarity between this formula and Pythagoras. The "a2 = b2 + c2" appears in both situations. The extra piece that appears in the cosine rule is the "- 2bc cos A" part, which is needed because the triangle is not right-angled. (cos 90 = 0, which is why this part of the formula doesn't appear when your triangle is right-angled).
So a handy way of remembering this formula is to recall Pythagoras, and then just remember to include "- 2bc cos A".
The important point on labelling your triangle is that angle A must be opposite length a, otherwise the formula will not work. It does not matter which way round the b and c are. The formula will still give the same answer.
You will need a scientific calculator in order to use the "cos" button. Make sure it is set to degrees.
Example
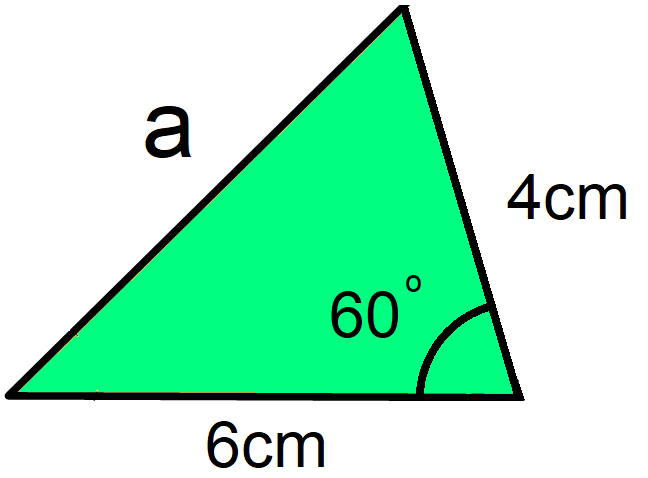
Calculate length a.
The first thing you should do is label the triangle and identify each value:
b = 4cm
c = 6cm
A = 60°
Remember, it doesn't matter which way round b and c are. Angle A is definitely 60° because it is opposite the length we want to calculate.
Now, it's a case of writing the formula:
a2 = b2 + c2 - 2bc cos A
Substituting your values:
a2 = 42 + 62 - (2 x 4 x 6 x cos 60)
(It is advisable to include brackets in this part of the formula, to make it easier to follow, and to ensure there are no mis-calculations).
Once you have typed this into your calculator and simplified, all that remains is to calculate a by square rooting:
a2 = 42 + 62 - (2 x 4 x 6 x cos 60)







