Solve Complex problems Using Pythagoras' Theorem

In this activity, you will use Pythagoras' Theorem in more complex ways than just finding one missing side of a right-angled triangle. 

 

Pythagoras recap

 

 

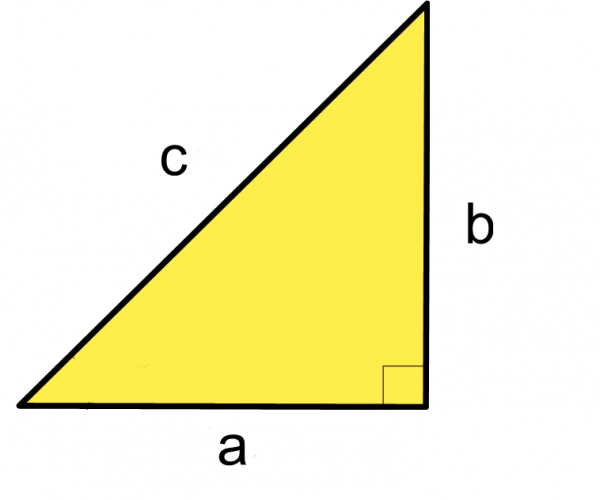
For a right-angled triangle you should be familiar with the rule

a² + b² = c²

 

For example, if lengths a = 10cm and b = 3cm, the hypotenuse, c, would be calculated as follows:

c² = 10² + 3² = 109

c = √109 = 10.44 cm (2 d.p.)

 

 

Complex Pythagoras

Now let's think about problems involving Pythagoras that are not as straightforward. Sometimes, you will have a shape with a right-angled triangle inside it, or you may need to use algebra when using the equation.

 

Example

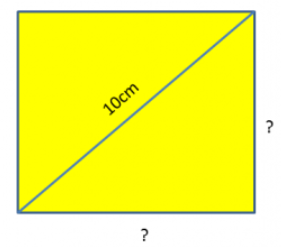
The diagonal of a square is 10 cm long.  What is the length of one side of the square?

 

 

The first thing to do is "find" the right-angled triangle inside the shape. It is fairly simple to see the hypotenuse is 10cm and length a and b are both unknown.

When dealing with the diagonal of a square, lengths a and b are equal.

If we call our unknown value "x" and substitute into the formula, we have:

x² + x² = 10²

 

This now becomes an equation:

2x² = 100

 

You need to solve for x by dividing by 2, and then square rooting: 

2x² = 100

x² = 50

x = √50

x = 7.07cm (2 d.p.)

 

 

This is just one example of a complex Pythagoras problem that involves needing to apply algebra to the formula. In more complex problems you will need to draw on other knowledge too.

The key idea is to sketch the situation out to turn a diagram into a right-angled triangle, substitute your known values into Pythagoras' formula, and then see if you can work out the missing lengths.